顶点形状

顶点形式转换计算器

计算器逐步确定二次函数的顶点形状。

一般二次函数

$y (x) = a x^{2} + b x + c$

转换为顶点形式

$y (x) = a {(x - x_{S})}^{2} + y_{S}$

输入二次函数的系数 a、b 和 c:

用二次加法转换为顶点形式:

结果就是顶点形状:

二次函数的顶点形式是:

$y (x) = a {(x - x_{S})}^{2} + y_{S}$

或者如果二次函数是正态形式，即 a=1:

$y (x) = {(x - x_{S})}^{2} + y_{S}$

其中 x_S 和 y_S 是抛物线顶点的 x 坐标和 y 坐标。顶点表示函数的最小值或最大值，取决于抛物线是向上还是向下开口。

p,q 形式的顶点

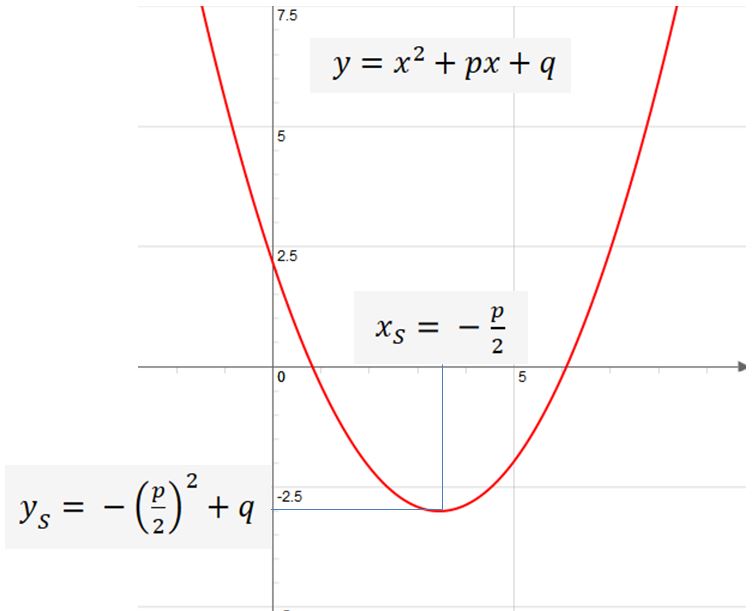
一般形式的顶点

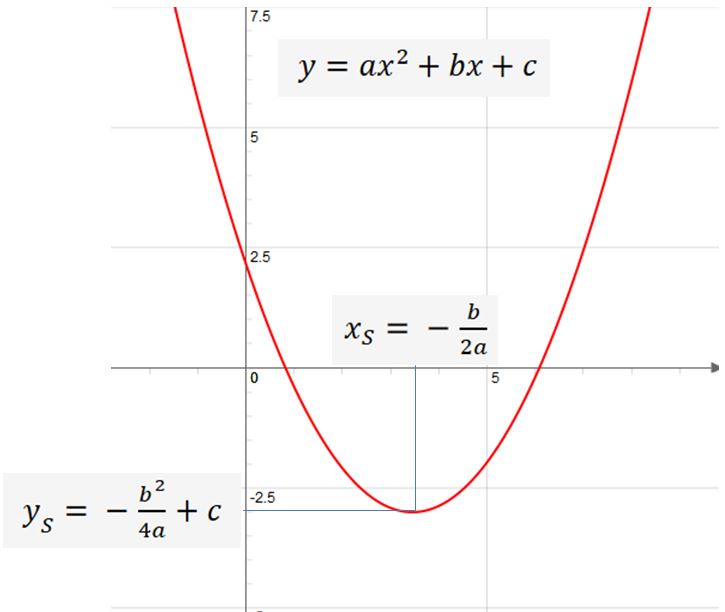
抛物线的顶点

二次函数的顶点是通过函数的导数确定的。极值的条件是函数的一阶导数消失。对于二次函数而言，这足以构成最小值或最大值。

起点是二次函数的一般形式:

$y (x) = a x^{2} + b x + c$

一般形式的推导过程是:

$y' = 2 a x + b$

顶点的条件是导数消失。这意味着下式适用：

$2 a x + b = 0$

解出 x 的方程，就得到了顶点的 x 坐标：

$x_{S} = - \frac{b}{2 a}$

将其插入一般二次函数，就能得到顶点的 y 坐标：

$y_{S} = - \frac{b^{2}}{4 a} + c$

二次函数的二阶导数显示了顶点是抛物线的最大值还是最小值。二次导数为

$y'' = 2 a$

因此，对于 a > 0，顶点是抛物线的最小值，而对于 a < 0，顶点是最大值。

从正则表达式到顶点表格的变换

在正则表达式中，x² 前面的系数等于 1。带常数 p 和 q 的二次函数的正则表达式如下：

$y (x) = x^{2} + p x + q$

如果二次函数为正态函数，则顶点为：

$x_{S} = - \frac{p}{2}$

$y_{S} = - {(\frac{p}{2})}^{2} + q$

通过二次加法和第一次二项式的应用，将正则表达式转换为顶点表格：

$x^{2} + p x + q =$

$x^{2} + p x + {(\frac{p}{2})}^{2} - {(\frac{p}{2})}^{2} + q =$

${(x + \frac{p}{2})}^{2} - {(\frac{p}{2})}^{2} + q =$

${(x - \frac{- p}{2})}^{2} - {(\frac{p}{2})}^{2} + q =$

${(x - x_{S})}^{2} + y_{S}$

从正则表达式转换为顶点表格的计算器

输入一元二次方程的系数 p 和 q：

用二次加法转换为顶点形式：

从一般形式到顶点形式的转换

系数为常数 a、b 和 c 的二次函数的一般形式：

$y = a x^{2} + b x + c$

如果二次函数为一般形式，则顶点的值为

$x_{S} = - \frac{b}{2 a}$

$y_{S} = - \frac{b^{2}}{4 a} + c$

用二次加法和第一次二项式的应用将一般形式转化为顶点形式：

$a x^{2} + b x + c =$

$a (x^{2} + \frac{b}{a} x) + c =$

$a (x^{2} + \frac{b}{a} x + {(\frac{b}{2 a})}^{2} - {(\frac{b}{2 a})}^{2}) + c =$

$a (x^{2} + \frac{b}{a} x + {(\frac{b}{2 a})}^{2}) - \frac{b^{2}}{4 a} + c =$

$a {(x + \frac{b}{2 a})}^{2} - \frac{b^{2}}{4 a} + c =$

$a {(x - \frac{- b}{2 a})}^{2} - \frac{b^{2}}{4 a} + c$

$a {(x - x_{S})}^{2} + y_{S}$

从顶点形状到一般形状

将二次函数的顶点形式转化为一般形式。

起点是顶点形状

$y = a {(x - x_{S})}^{2} + y_{S} =$

求解平方的结果是

$a (x^{2} - 2 x x_{S} + {x_{S}}^{2}) + y_{S} =$

乘去括号，得出

$a x^{2} - 2 a x x_{S} + a {x_{S}}^{2} + y_{S} =$

插入 x_S 和 y_S 的结果：

$a x^{2} + 2 a x \frac{b}{2 a} + a {(- \frac{b}{2 a})}^{2} - \frac{b^{2}}{4 a} + c =$

缩短结果：

$a x^{2} + b x + \frac{b^{2}}{4 a} - \frac{b^{2}}{4 a} + c =$

总和相互抵消，得出一般二次函数：

$a x^{2} + b x + c$

根据顶点形式计算零点

根据顶点形式很容易确定二次函数的零点。

起点是顶点形状

$y = a {(x - x_{S})}^{2} + y_{S}$

条件是函数必须为零

$0 = a {(x - x_{S})}^{2} + y_{S}$

转变的结果是

${(x - x_{S})}^{2} = - \frac{y_{S}}{a}$

和平方根得出

$x - x_{S} = \pm \sqrt{- \frac{y_{S}}{a}}$

从而最终得到零点

$x_{1,2} = x_{S} \pm \sqrt{- \frac{y_{S}}{a}}$