Gráficos de coloración de dominios de funciones complejas
Ajustes básicos del plotter
Tono (Hue)

El tono se selecciona en función del ángulo.
Luminosidad
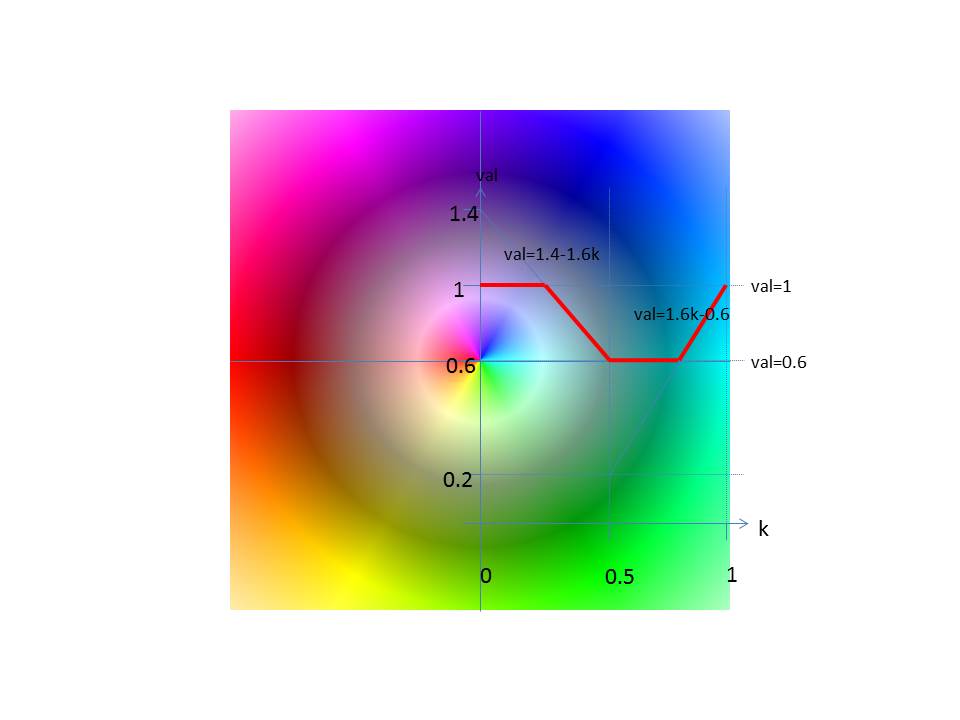
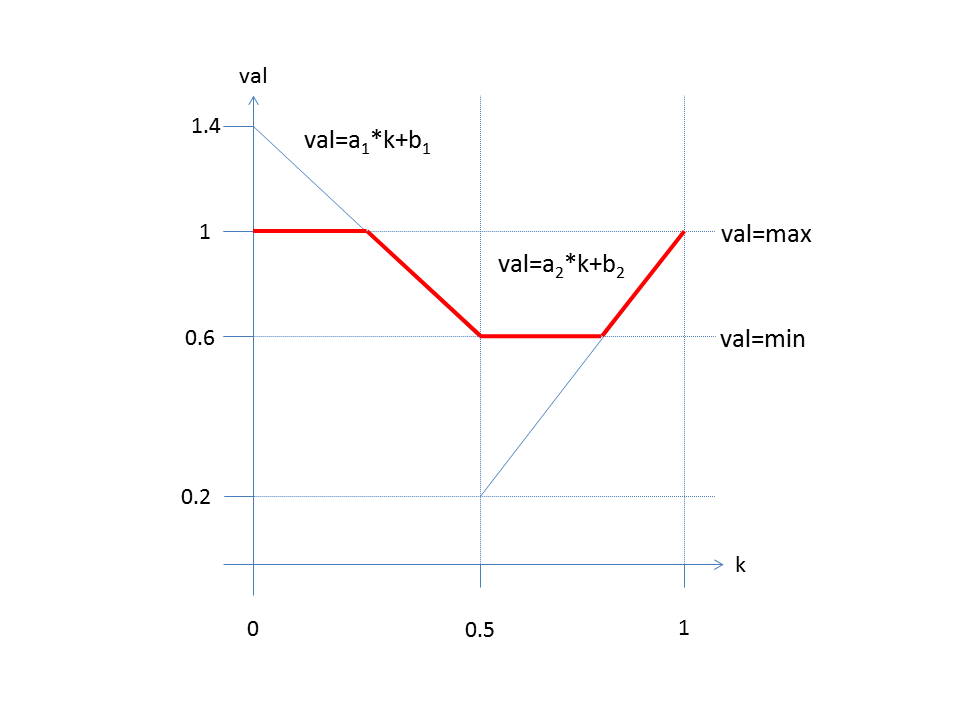
La luminosidad se determina según el siguiente diagrama.
En el intervalo [0,0,5) se aplica val = a1 * k + b1
En el intervalo [0,5,1) aplica val = a2 * k + b2
Es: min ≤ val ≤ max
Saturación
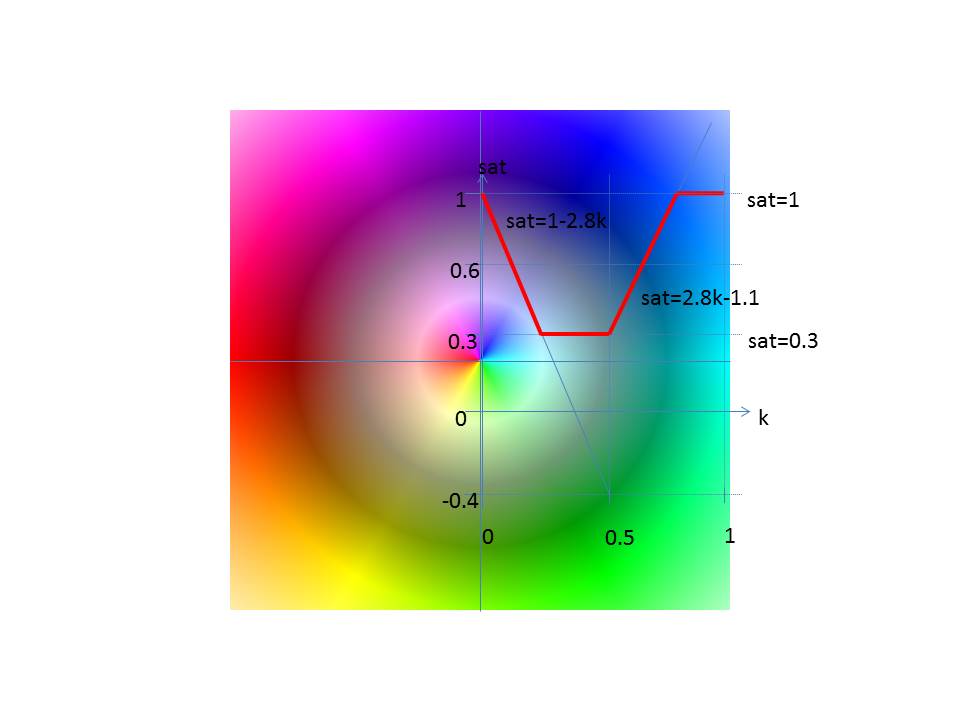
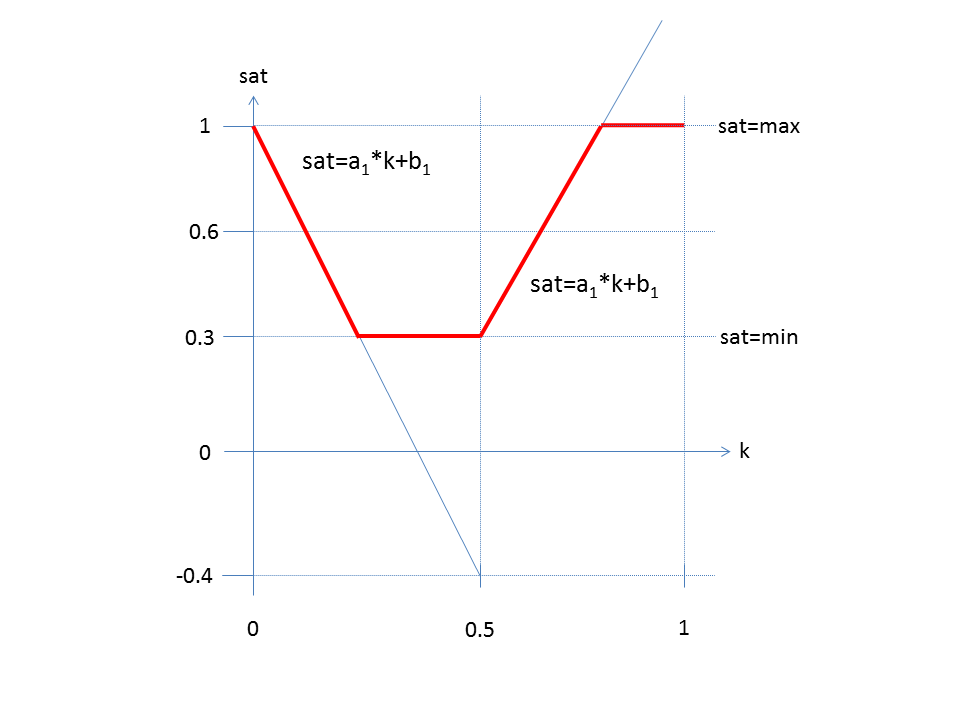
La saturación se determina según el siguiente diagrama.
En el intervalo [0,0,5) se aplica sat = a1 * k + b1
En el intervalo [0,5,1) aplica sat = a2 * k + b2
Es: min ≤ sat ≤ max
Selección de una combinación de colores:
Establecer la anchura y la altura de la parcela:
Ajuste del gradiente de saturación:
Ajuste del gradiente de luminosidad:
Representación de funciones complejas
Función lineal compleja
Parte real de f(z):
Parte imaginaria de f(z):
Cantidad de f(z):
Argumento φ de f(z):
Función compleja cuadrada
Parte real de f(z):
Parte imaginaria de f(z):
Cantidad de f(z):
Argumento φ de f(z):
Función compleja racional fraccionaria
Parte real de f(z):
Parte imaginaria de f(z):
Cantidad de f(z):
Argumento φ de f(z):
Función lineal fraccionaria
Parte real de f(z):
Parte imaginaria de f(z):
La función f es una composición de las anteriores f=f1+f2 y así las partes real e imaginaria resultan de la suma de las funciones individuales f1 y f2.
Parte real de f(z):
Parte imaginaria de f(z):
e-Función compleja
Parte real de f(z):
Parte imaginaria de f(z):
Cantidad de f(z):
Argumento φ de f(z):
exp(z) / (z-a)
La función f es un producto de dos funciones f=f1 * f2 y entonces el resultado real e imaginario sigue:
Parte real de f(z):
Parte imaginaria de f(z):
exp(z)/(z-a) + (z+b)/(z+c)
La función f es un producto de dos funciones f=f1 * f2 y entonces el resultado real e imaginario sigue:
Parte real de f(z):
Parte imaginaria de f(z):
La función f también es la suma de dos funciones f=f1+f2 y, por tanto, la parte real e imaginaria resulta de la suma de f1 y f2.
Parte real de f(z):
Parte imaginaria de f(z):
Función sinusoidal compleja
Parte real de f(z):
Parte imaginaria de f(z):
Cantidad de f(z):
Argumento φ de f(z):
x2 + i y2
Parte real de f(z):
Parte imaginaria de f(z):
Cantidad de f(z):
Argumento φ de f(z):
Generalidades
La teoría de las funciones investiga las funciones de variable compleja así que los números complejos cuyo rango de valores son también números complejos. Los números complejos son una extensión de los números reales en el espacio bidimensional. Muchas reglas computacionales de los números reales se pueden aplicar a los números complejos. Fue justificada, la teoría de las funciones complejas principalmente por Augustin-Louis Cauchy, Bernhard Riemann, y Karl Weierstrass.
Coloración de dominios
El método de la rueda de colores es un método para representar gráficamente funciones complejas. Las funciones complejas representan a su vez el plano complejo bidimensional, los valores reales e imaginarios. El método de la rueda de colores utiliza la cantidad r = |f(z)| y el ángulo φ el valor de la función compleja f(z) aroy el color de visualización del conjunto de valores de la función. De acuerdo con r y φ el valor de la función se selecciona el color de la rueda de color. La cantidad define la saturación y el módulo se asigna a intervalos . El primer intervalo es 0 .. 1 luego siguen los intervalos ( 1 .. e] , (e .. e 2 ] , (e 2 ... e 3 ], etc. el color se define por el ángulo y en 6 zonas de color comenzando con split azul de 0° a 60° y terminando con verde de 300° a 360°. el método está diseñado para que los valores de la función están cerca entre sí también se muestran de color similar. mapear las sumas en intervalos de la potencia de e corresponde a una representación logarítmica.
Rueda de colores
Una compilación de una rueda de colores se puede armar desde diferentes puntos dependiendo del estado de cosas que se quiera visualizar. La base del círculo cromático es la percepción de colores similares. Dejando a los sujetos con el patrón de color normal de acuerdo con la sensación en la clase de similitud, que los tonos se traen generalmente en el mismo orden. Principio y final de la serie son aroand tan similar que la serie se puede cerrar para formar un círculo.
Plano de Gauss
Los números complejos son bidimensionales y se pueden utilizar como vectores en el plano de Gauss de los números representan. En el eje horizontal (Re) de la parte real y en el eje vertical se aplica (Im) de la parte imaginaria del número complejo. Los vectores también pueden ser similares al número complejo en coordenadas cartesianas (x, y) o coordenadas polares (r, φ) se puede expresar. En el método del círculo cromático se utilizan coordenadas polares y la rueda de color se sitúa en el plano del intervalo de manera número gaussiano.
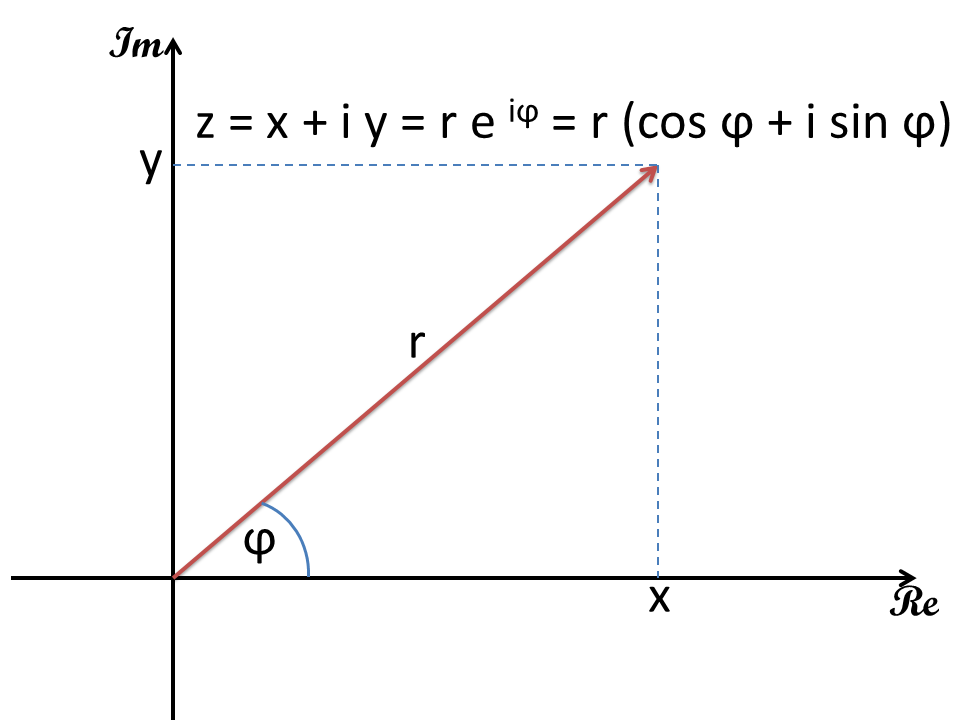
Más calculadoras
Calculadoras:
Contenido Calculadora de derivados, gradiente y derivadas parciales Diferenciación de fracciones Derivación de las funciones raíz Derivación de las funciones trigonométricas Determinante NxN EDO de línea primer orden EDO segundo orden Trigonometría calculadora Serie de Fourier Ajuste de curvas Calculadora de números complejos