Calculadora trigonometría en línea

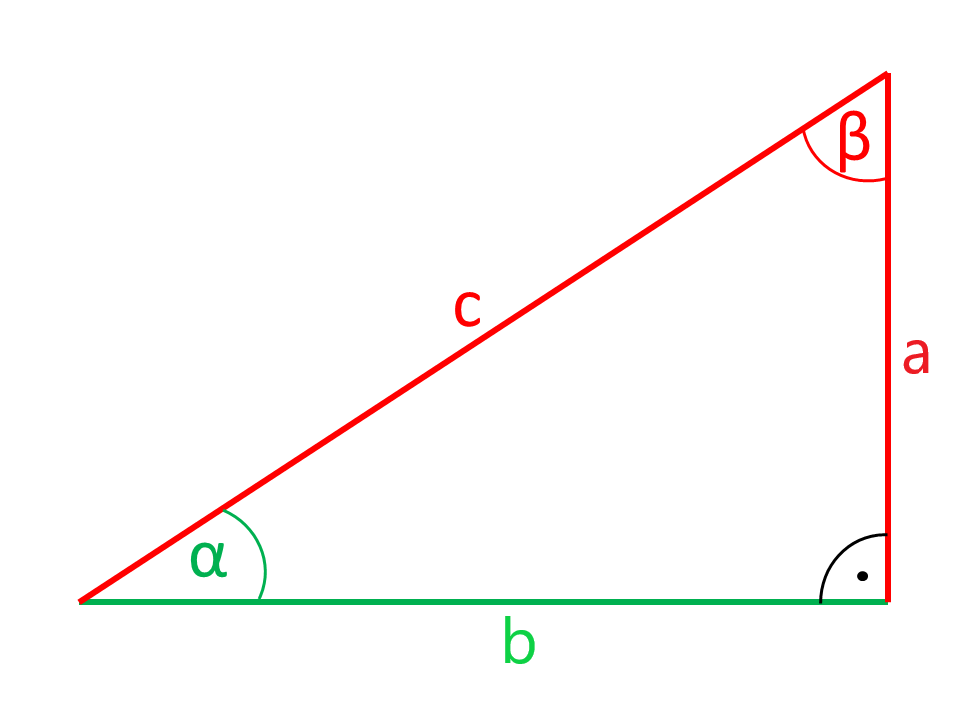
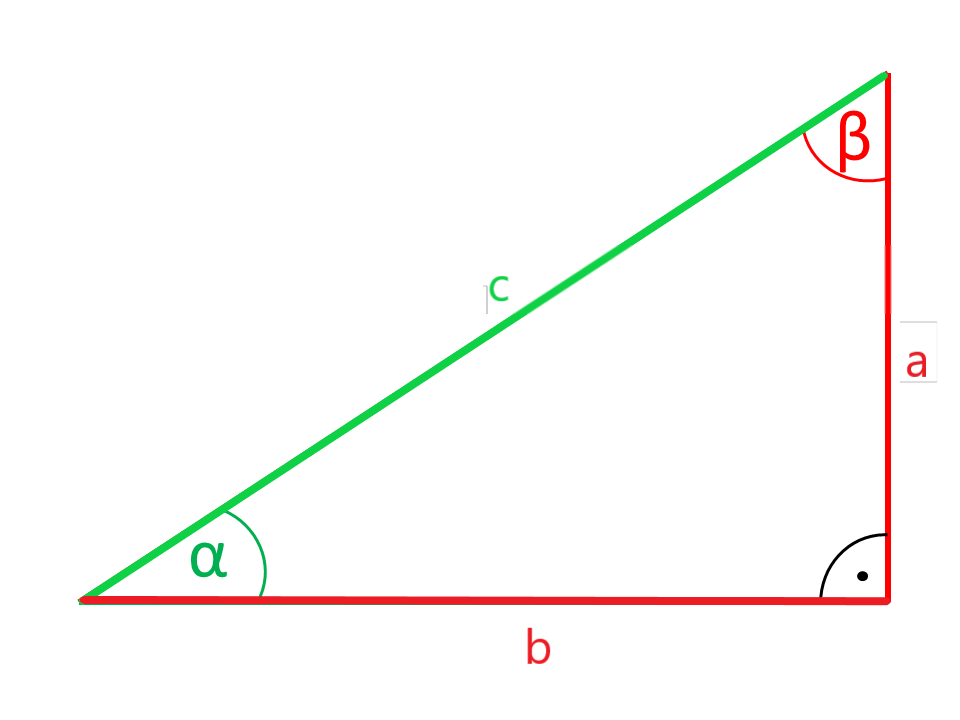
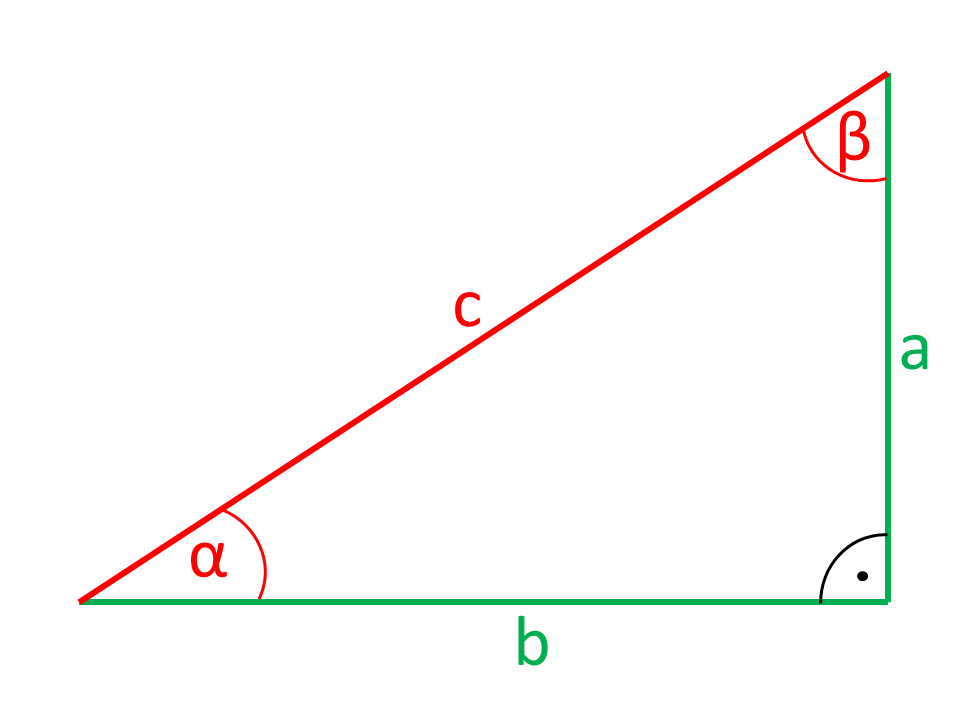
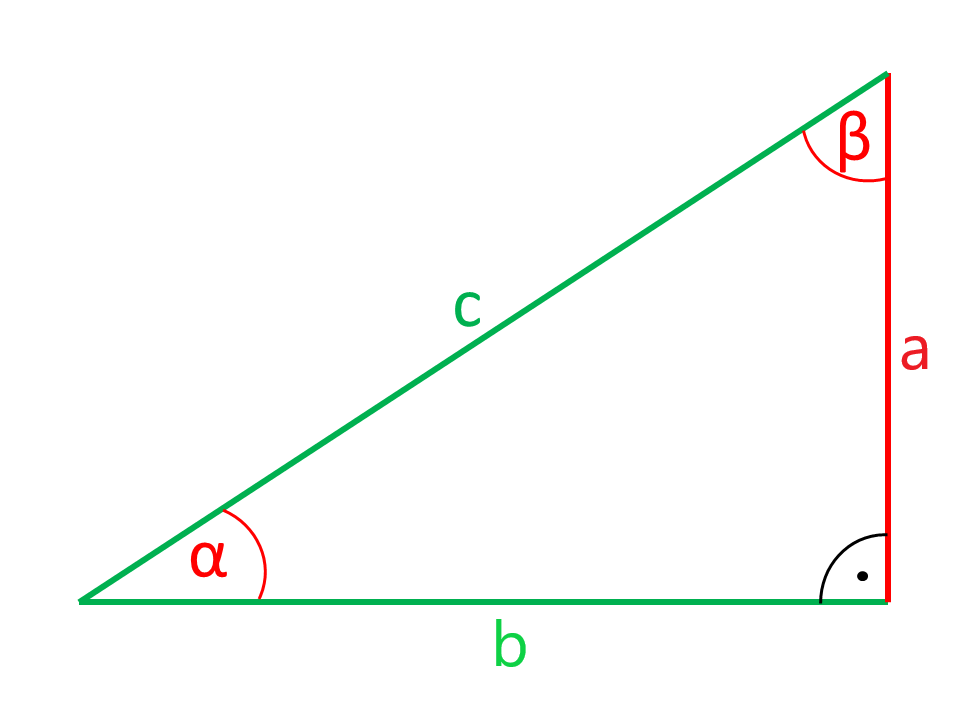
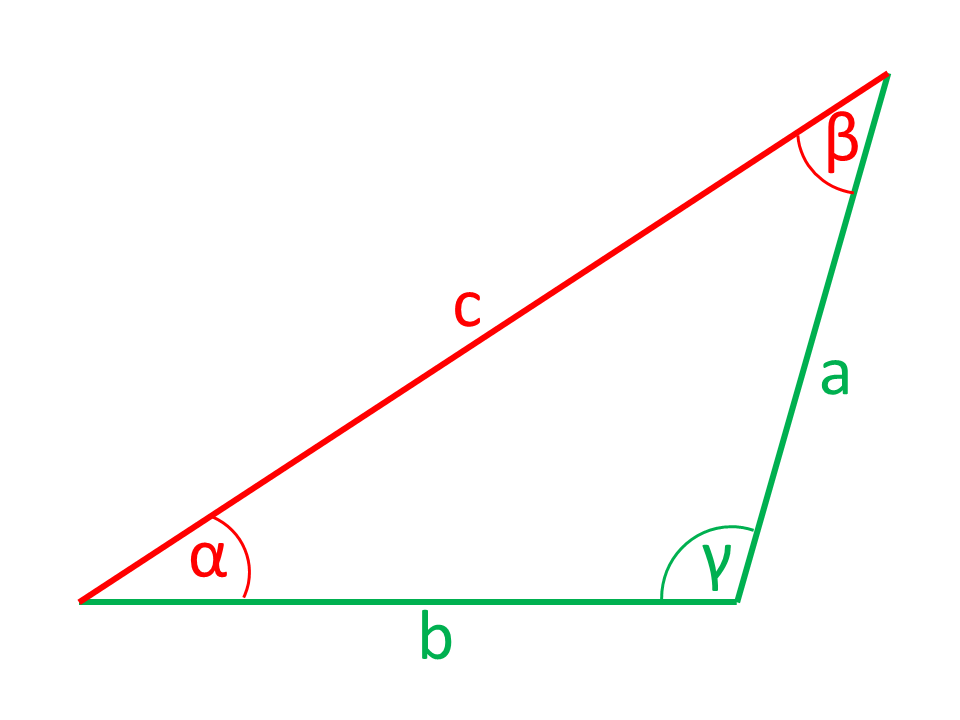
Calculadora de triángulo rectangular

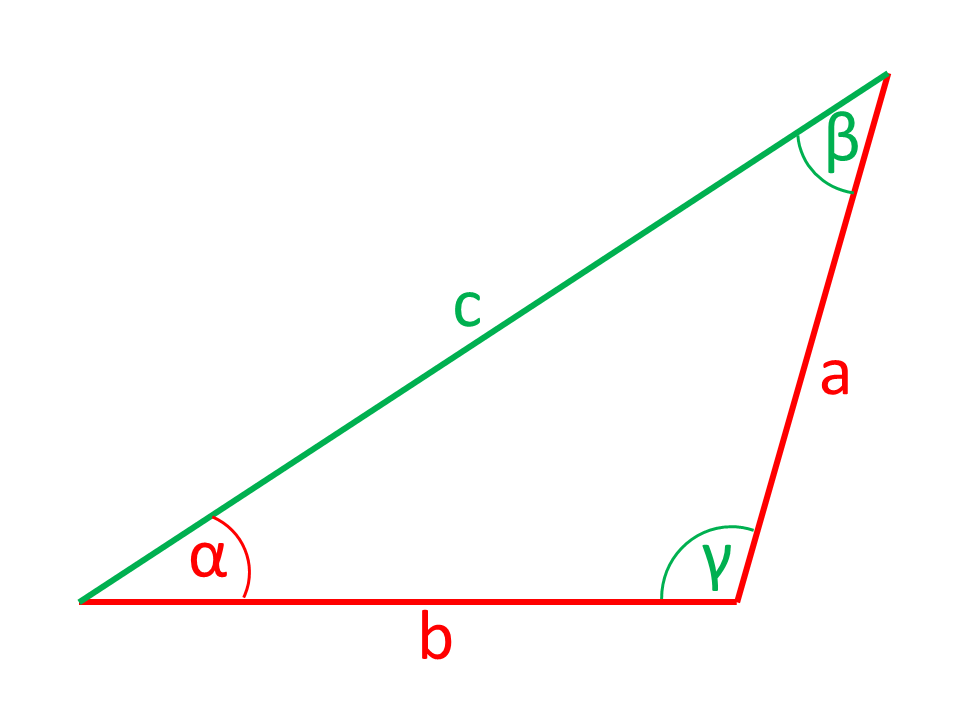
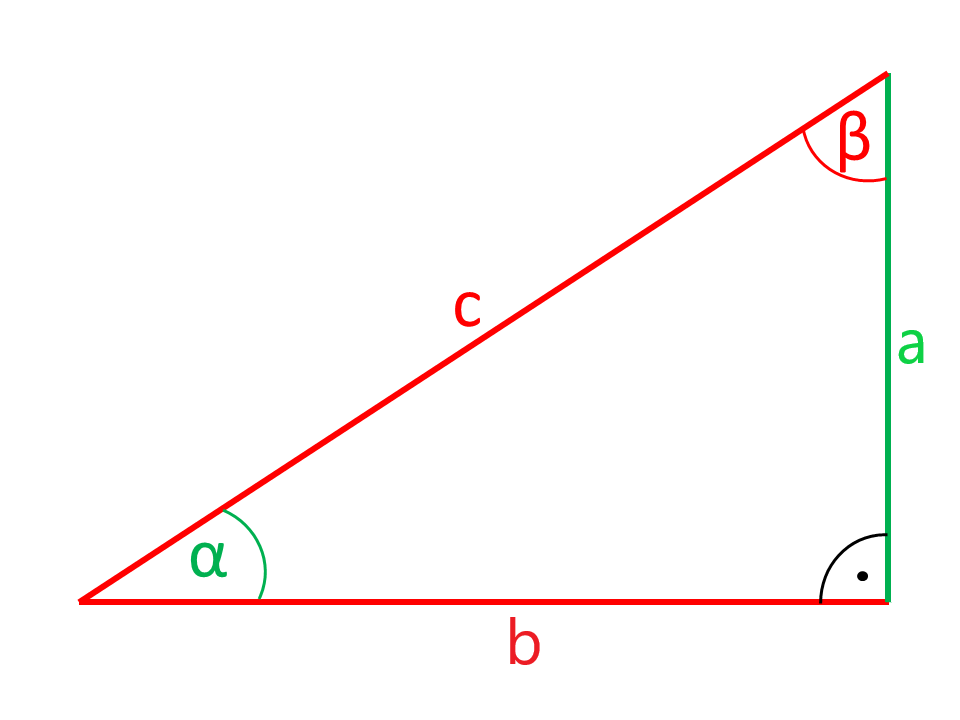
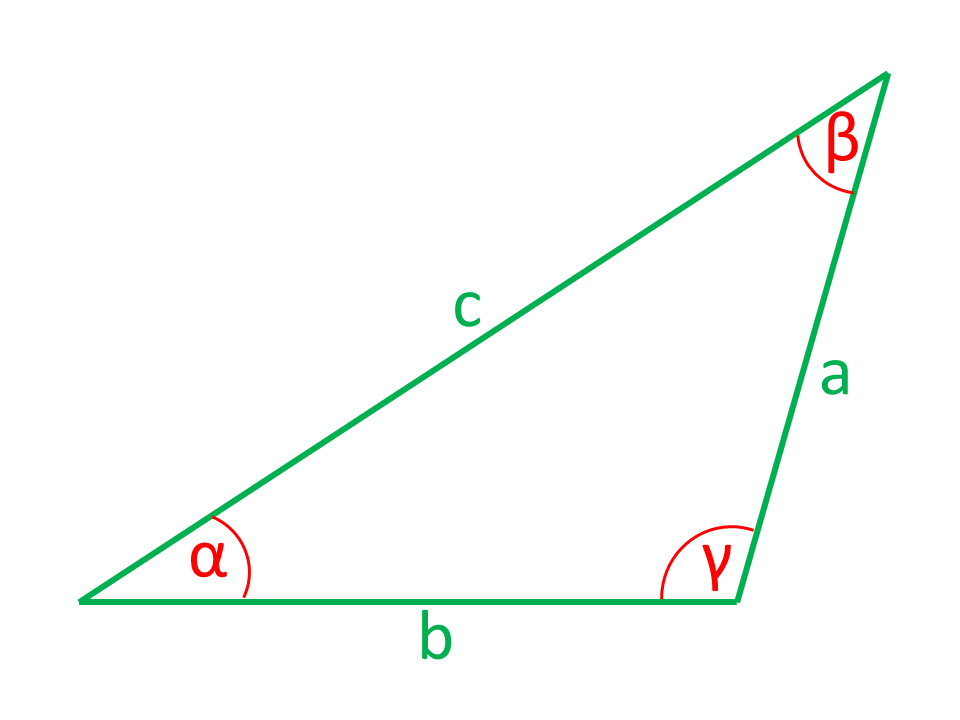
Los lados o ángulos que se muestran en las ilustraciones en color rojo son calculados por la calculadora a partir de los lados y ángulos que se muestran en color verde.

Ángulo y cateto opuesto

α en grado =

a =

Ángulo y cateto adyacente

α en grado =

b =

Ángulo y hipotenusa

α en grado =

c =

Cathetus

a =

b =

Cateto y hipotenusa

b =

c =

Calculadora de triángulos generales

Dos lados y un ángulo

γ en grado =

a =

b =

Dos ángulos y un lado

γ en grado =

β en grado =

c =

Tres lados

a =

b =

c =

Ejemplos de cálculos trigonométricos

A continuación se presentan algunos ejemplos que ilustran la aplicación de las fórmulas trigonométricas.

Ejemplo: Cálculo de la altura de la torre

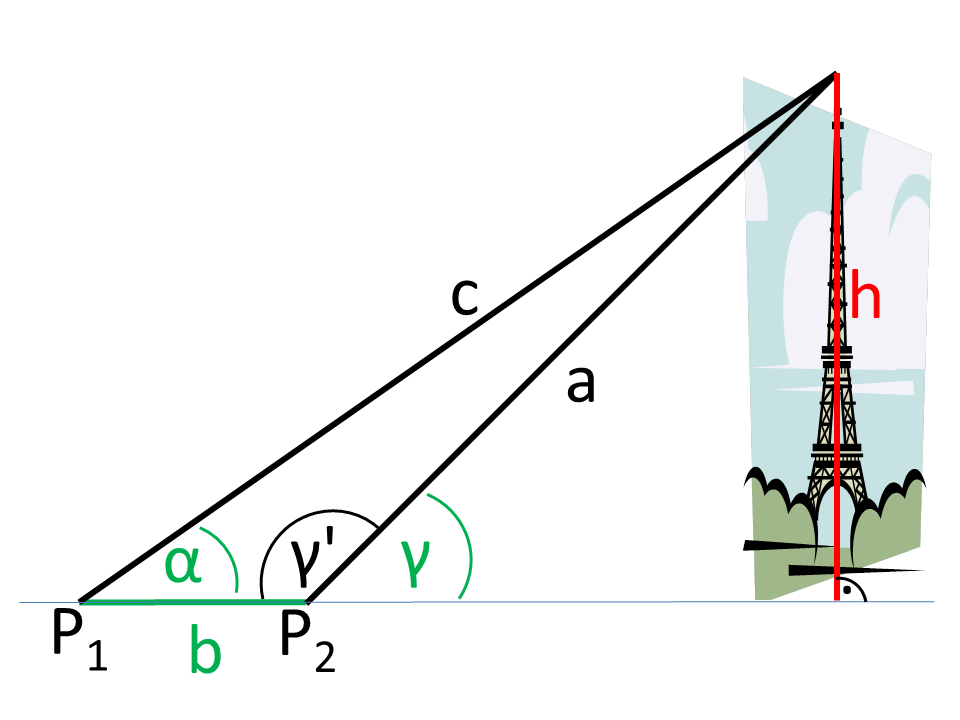
El ejemplo muestra cómo se puede determinar una altura, aunque no sea posible el acceso directo.

La figura muestra que los ángulos de visión (α, γ) y la distancia b de las posiciones se determinaron a partir de dos posiciones (P₁, P₂) (verde en la Ilustración).

Se forma un triángulo a partir de P₁, P₂, y la punta de la torre. De este triángulo general se conoce el ángulo &alfa; y el lado b. El ángulo γ se puede calcular de la siguiente manera:

$\mathrm{\gamma \text{'}}=180-\mathrm{\gamma }$

El ángulo que aún falta β se puede determinar, ya que la suma angular en el triángulo es de 180°.

$\beta =180-\mathrm{\alpha }-\mathrm{\gamma \text{'}}=\mathrm{\gamma }-\mathrm{\alpha }$

El lado a es un lado común del triángulo general y del triángulo rectángulo formado por a y la altura de la torre y la línea base.

$a=\sin \left(\alpha \right)\frac{b}{\sin \left(\beta \right)}=b\frac{\sin \left(\alpha \right)}{\sin \left(\gamma -\alpha \right)}$

En el triángulo rectángulo, a es la hipotenusa, y h es el cateto opuesto del ángulo γ. Así, la altura deseada h puede calcularse con la función angular.

$h=a\sin \left(\gamma \right)=b\frac{\sin \left(\alpha \right)\sin \left(\gamma \right)}{\sin \left(\gamma -\alpha \right)}$

Alternativamente, la altura de la torre también se puede calcular aplicando dos ecuaciones para el triángulo rectángulo. El primer triángulo está formado por P₁ y la base de la torre, así como la punta de la torre. El segundo análogo sale de P₂.

Lo es:

$\tan \gamma =\frac{h}{x}$

y

$\tan \alpha =\frac{h}{b+x}$

con la distancia desconocida x desde P₂ hasta el punto base de la torre.

La remodelación de las ecuaciones resulta en cada caso:

$x=\frac{h}{\tan \gamma }$

y

$x=\frac{h-b\tan \alpha }{\tan \alpha }$

Igualando las ecuaciones y resolviendo para h se obtiene la solución:

$h=b\frac{\tan \alpha \tan \gamma }{\tan \gamma -\tan \alpha }$

Las dos soluciones para h son equivalentes se puede demostrar fácilmente con la sustitución de

$\tan \left(\alpha \right)=\frac{\sin \left(\alpha \right)}{\cos \left(\alpha \right)}$

y

$\tan \left(\gamma \right)=\frac{\sin \left(\gamma \right)}{\cos \left(\gamma \right)}$

$h=b\frac{\tan \alpha \tan \gamma }{\tan \gamma -\tan \alpha }=b\frac{\sin \alpha \sin \gamma }{\sin \gamma \cos \alpha -\sin \alpha \cos \gamma }$

Con el teorema de la adición

$\sin \left(x\pm y\right)=\sin \left(x\right)\cos \left(y\right)\pm \cos \left(x\right)\sin \left(y\right)$

los resultados de la solución anterior.

Lo es:

$h=b\frac{\tan \alpha \tan \gamma }{\tan \gamma -\tan \alpha }=b\frac{\sin \left(\alpha \right)\sin \left(\gamma \right)}{\sin \left(\gamma -\alpha \right)}$

Ejemplo: Rodamiento cruzado

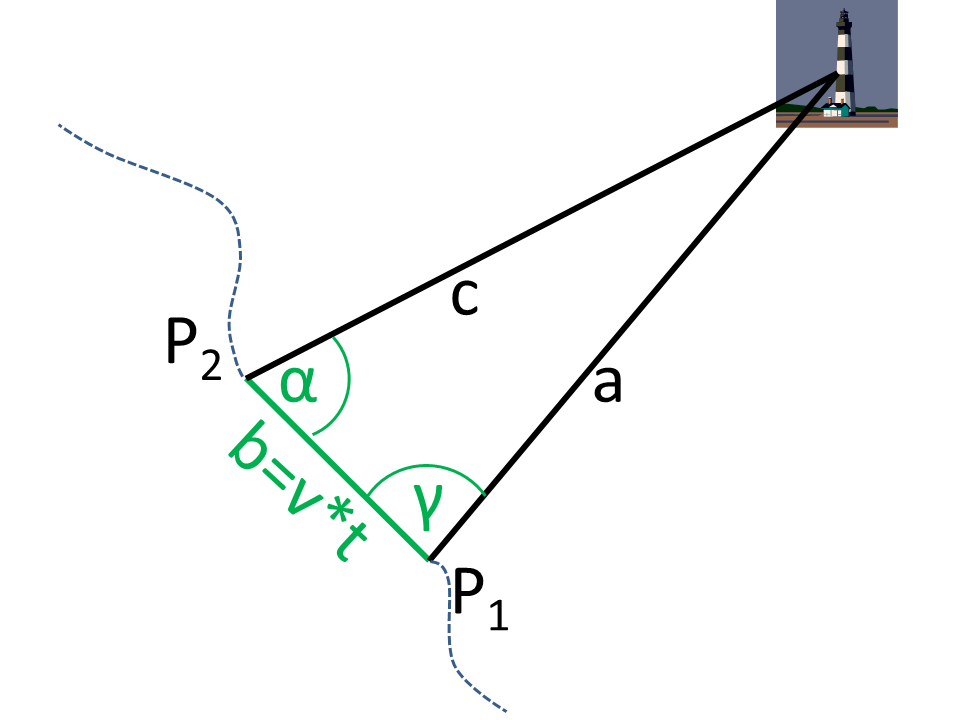
Un punto fijo (por ejemplo, un faro) desde dos posiciones se dirige al rodamiento transversal. Se aplica un rumbo y una velocidad constantes entre las dos rumbos (P₁, P₂). Entonces, la distancia del punto de destino puede determinarse a partir de los rumbos.

La figura muestra que los ángulos de visión (α, γ) relativos a la dirección de desplazamiento se determinaron en dos posiciones (P₁, P₂) (en verde en la figura). La longitud lateral b se obtiene a partir de la velocidad v y el intervalo de tiempo t de las mediciones.

Se forma un triángulo a partir de P₁, P₂ y el punto objetivo (faro). A partir de este triángulo general, se conoce el ángulo α y el lado b = v ⋅ t.

El ángulo que aún falta β se puede determinar, ya que la suma angular en el triángulo es de 180°.

$\beta =180-\mathrm{\alpha }-\mathrm{\gamma }$

En el siguiente paso, se utiliza la regla de los senos para calcular el lado a. El lado a es la distancia desde el punto de medición P₁.

$a=\sin \left(\alpha \right)\frac{b}{\sin \left(\beta \right)}$

La distancia al segundo punto de medición se calcula de forma análoga.

$c=\sin \left(\gamma \right)\frac{a}{\sin \left(\alpha \right)}$

Ejemplo: Medición de una ruta inaccesible (tarea de Hansen)

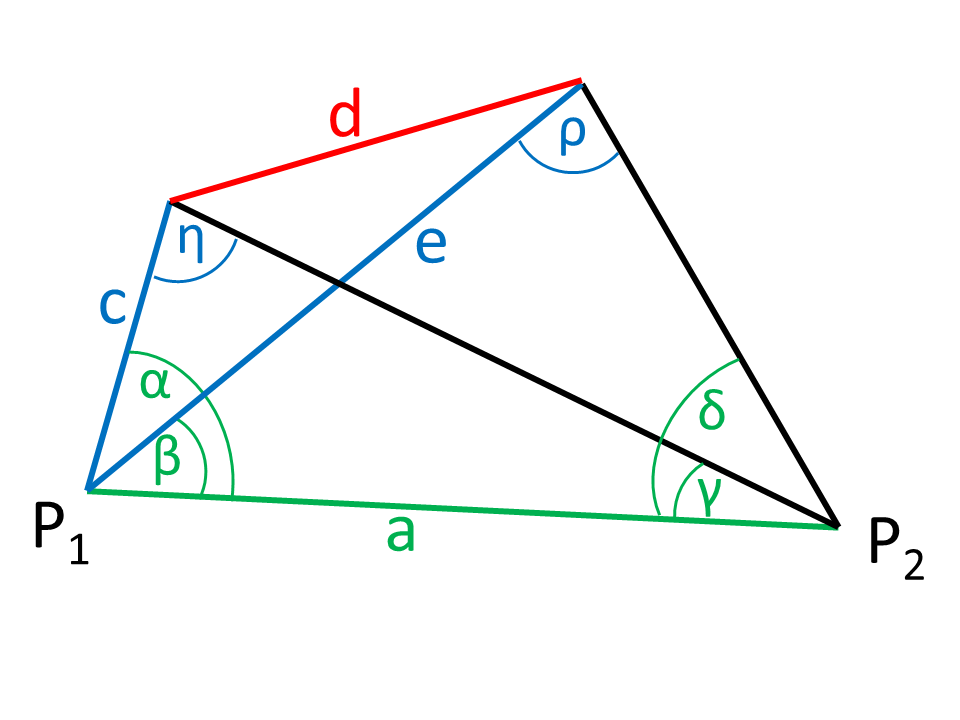
Para medir una ruta inaccesible, el inicio y el final de la ruta se determinan a partir de dos puntos (P₁, P₂).

La figura muestra que los ángulos de visión (α, β, γ, δ) en dos posiciones (P₁, P₂) respecto al eje de unión de los puntos (verde en la figura). También se conoce la distancia a de los puntos de medición. Hay que determinar la longitud de la distancia inaccesible d (rojo en la figura).

La figura muestra los valores azules que hay que calcular.

El ángulo η se puede determinar, ya que la suma angular en el triángulo es de 180°.

$\eta =180-\mathrm{\alpha }-\mathrm{\gamma }$

En el siguiente paso, se utiliza la regla del seno para calcular el lado c.

$c=a\frac{\sin \left(\gamma \right)}{\sin \left(\eta \right)}$

El lado e también se calcula con la regla del seno.

$e=a\frac{\sin \left(\delta \right)}{\sin \left(\rho \right)}$

El ángulo ρ resulta de la suma de ángulos en un triángulo.

$\rho =180-\mathrm{\beta }-\mathrm{\delta }$

Ahora se puede utilizar la regla del coseno para calcular la distancia d necesaria.

$d^2=a^2+c^2-2ac\cos \left(\alpha -\beta \right)$

Ejemplo: Triángulo de fuerzas sobre el péndulo

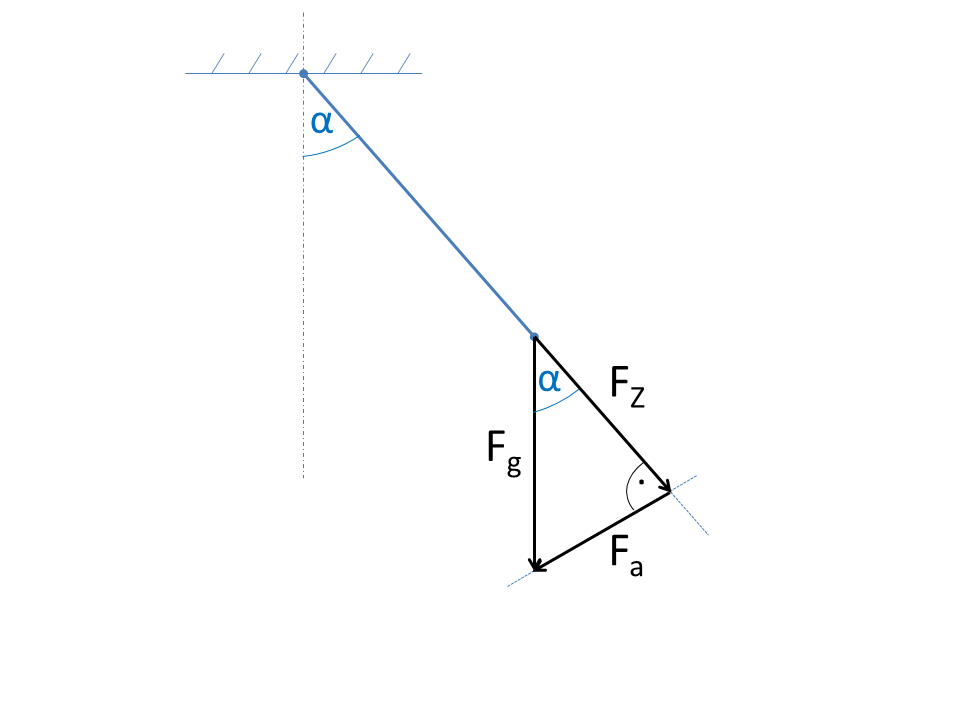
La descomposición de las fuerzas en componentes ortogonales desempeña un papel importante en la mecánica. Este ejemplo muestra cómo la fuerza del peso puede descomponerse en dos componentes mediante las funciones angulares.

La figura muestra un péndulo de hilo con una masa en el extremo del hilo. La fuerza del peso F_g debe descomponerse en fuerzas parciales. La fuerza en la dirección del hilo F_Z no contribuye a la aceleración y la fuerza F_a es, por tanto, relevante para la ecuación de movimiento.

Los esfuerzos parciales pueden especificarse directamente mediante las funciones angulares, ya que son un triángulo rectángulo.

$F_a=F_g\sin \left(\alpha \right)$

$F_Z=F_g\cos \left(\alpha \right)$

Trigonometría general

La tarea básica de la trigonometría es (etc. Longitudes de los lados, tamaños de los ángulos, longitudes de los triángulos-transversales) que se calculan a partir de tres tamaños de un triángulo dado otros tamaños de este triángulo. Como ayuda a las funciones trigonométricas seno (sin), coseno (cos), tangente (tan), Cotangente (cot). El precursor de la trigonometría ya existía durante la Antigüedad en las matemáticas griegas. Aristarco de Samos aprovechó las propiedades de los triángulos rectángulos para calcular las relaciones de distancia entre la tierra y el sol y la luna.

Triángulo rectángulo

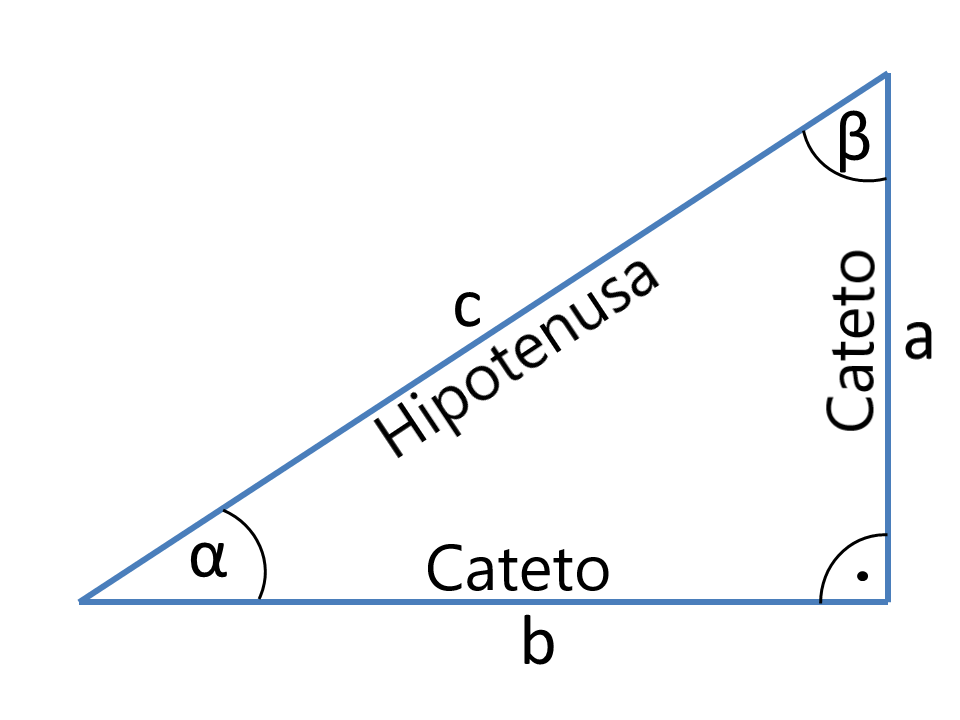
Definiciones

Los lados a y b del triángulo rectángulo, que incluyen el ángulo recto son los catetos. El ángulo recto opuesto al lado c es la hipotenusa. Mirando el ángulo α como el lado a es el lado adyacente y el lado opuesto b.

Funciones trigonométricas

$\sin \left(\alpha \right)=\cos \left(\beta \right)=\frac{a}{c}$

$\cos \left(\alpha \right)=\sin \left(\beta \right)=\frac{b}{c}$

$\tan \left(\alpha \right)=\cot \left(\beta \right)=\frac{a}{b}$

Grados / Radianes

El ángulo puede especificarse en grado (deg) o en radianes (rad). El círculo completo en grado es de 360 grados, en radianes es de 2π. En consecuencia, se aplican las siguientes conversiones.

$\text{Ángulo (rad)}=\frac{\pi }{180}\text{Angle (deg)}$

$\text{Ángulo (deg)}=\frac{180}{\pi }\text{Angle (rad)}$

Suma de ángulos

La suma de los ángulos de un triángulo es 180°. Esto se aplica en el triángulo rectángulo la siguiente relación para el ángulo.

$90=\alpha +\beta$

Triángulo general

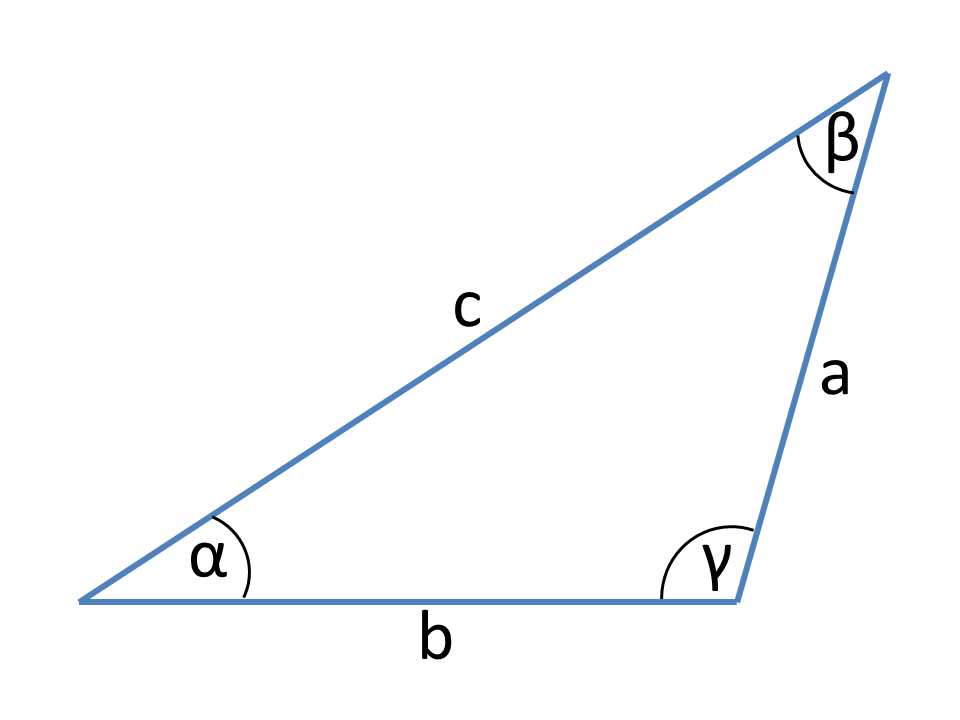
Definiciones

Esencial para los cálculos en triángulo general son la ley del coseno y del seno y la relación de las funciones trigonométricas.

Ley del seno

$\frac{a}{\sin \left(\alpha \right)}=\frac{b}{\sin \left(\beta \right)}=\frac{c}{\sin \left(\gamma \right)}$

Ley del coseno

$a^2=b^2+c^2-2bc\cos \left(\alpha \right)$

$b^2=a^2+c^2-2ac\cos \left(\beta \right)$

$c^2=a^2+b^2-2ab\cos \left(\gamma \right)$

Ley de proyección

$c=a\cdot \cos \left(\beta \right)+b\cdot \cos \left(\alpha \right)$

Fórmula de la tangente

$\tan \left(\gamma \right)$$=\frac{c\cdot \sin \left(\alpha \right)}{b-c\cdot \cos \left(\alpha \right)}$$=\frac{c\cdot \sin \left(\beta \right)}{a-c\cdot \cos \left(\beta \right)}$

Suma de ángulos

La suma de los ángulos de un triángulo beträt 180°.

$180=\alpha +\beta +\gamma$

Circumradio r

$r=\frac{s}{4\cdot \cos \left(\frac{\alpha }{2}\right)\cdot \cos \left(\frac{\beta }{2}\right)\cdot \cos \left(\frac{\gamma }{2}\right)}$

con

$s=\frac{1}{2}\left(a+b+c\right)$

Radio del círculo inscrito ρ

$\rho =\sqrt{\frac{\left(s-a\right)\left(s-b\right)\left(s-c\right)}{s}}$

Altura h_c en c

$h_c=a\cdot \sin \left(\beta \right)=b\cdot \sin \left(\alpha \right)$

Área A

$A=\frac{1}{2}a\cdot b\cdot \sin \left(\gamma \right)$

Fórmula del área de Heronische

$A=\rho s=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}$

Propiedades de las funciones trigonométricas

Fórmulas reductoras (en Grado)

$\sin \left(\mathrm{90°}+x\right)=\cos \left(x\right)$

$\cos \left(\mathrm{90°}+x\right)=-\sin \left(x\right)$

$\tan \left(\mathrm{90°}+x\right)=-\cot \left(x\right)$

$\cot \left(\mathrm{90°}+x\right)=-\tan \left(x\right)$

$\sin \left(\mathrm{180°}+x\right)=-\sin \left(x\right)$

$\cos \left(\mathrm{180°}+x\right)=-\cos \left(x\right)$

$\tan \left(\mathrm{180°}+x\right)=\tan \left(x\right)$

$\cot \left(\mathrm{180°}+x\right)=\cot \left(x\right)$

Funciones trigonométricas con argumentos iguales

${\sin \left(x\right)}^2+{\cos \left(x\right)}^2=1$

$\tan \left(x\right)=\frac{\sin \left(x\right)}{\cos \left(x\right)}$

Teorema de la adición de funciones trigonométricas

$\sin \left(x\pm y\right)=\sin \left(x\right)\cos \left(y\right)\pm \cos \left(x\right)\sin \left(y\right)$

$\cos \left(x\pm y\right)=\cos \left(x\right)\cos \left(y\right)\mp \sin \left(x\right)\sin \left(y\right)$

$\tan \left(x\pm y\right)=\frac{\tan \left(x\right)\pm \tan \left(y\right)}{1\mp \tan \left(x\right)\tan \left(y\right)}$

Más calculadoras

Calculadoras:

Contenido Calculadora de triángulo Trigonometría tabla Potencia de funciones trigonométricas