Online graphically difference of vectors

Subtraction of two two-dimensional Vectors v and w

The operation with the vectors is graphically presented. By moving the vector endpoints the vectors can be changed. The red vector is the result of the vector subtraction. The dotted line is the parallel moved and inverted vector.

⃢

↹#.000

🔍↔

🔍↕

v_x =

v_y =

w_x =

w_y =

Subtraction of vectors

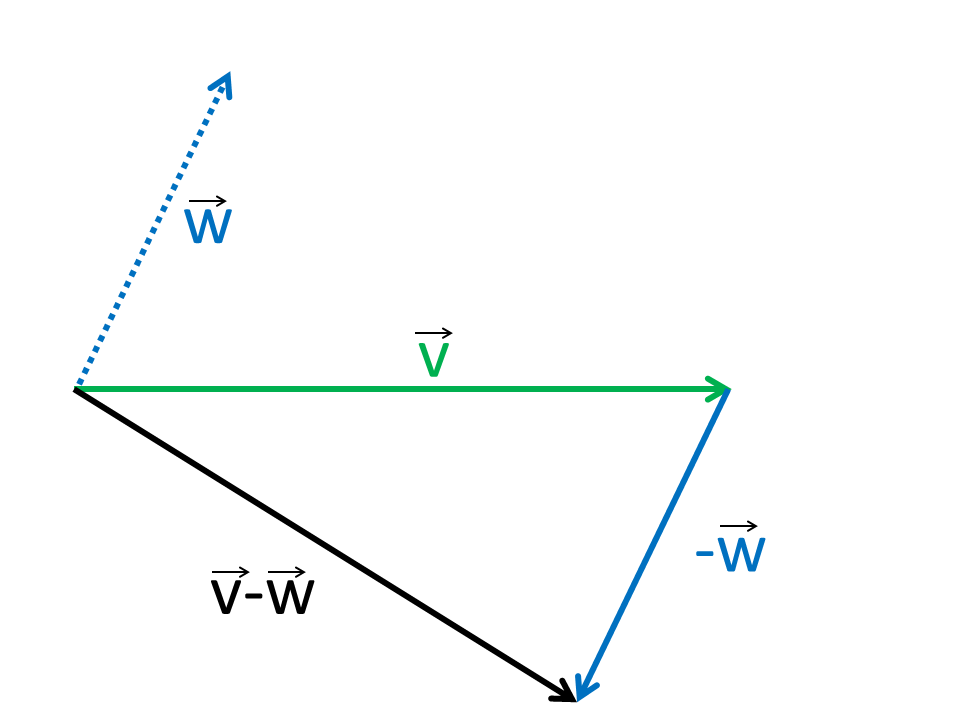
The subtraction of vectors is done in Cartesian coordinates componentwise.

Geometrically, the construction is similar to the addition of only the vector will be mirrored to the negative sign in the vector direction.

$\vec{v} - \vec{w} = (\begin{matrix} v_{1} \\ v_{2} \\ ⋮ \\ v_{n} \end{matrix}) - (\begin{matrix} w_{1} \\ w_{2} \\ ⋮ \\ w_{n} \end{matrix}) = (\begin{matrix} v_{1} - w_{1} \\ v_{2} - w_{2} \\ ⋮ \\ v_{n} - w_{n} \end{matrix})$

Screenshot of the Image

Print or save the image via right mouse click.

More Calculators

Here is a list of of further useful calculators:

Vector calculation Vector addition Vector subtraction Matrix-Vector product Inner product Complex numbers graphical Addition complex numbers graphical Multiplication complex numbers graphical Division complex numbers graphical Power complex numbers graphical