Online graphically sum of vectors

Addition of two two-dimensional Vectors v and w

The operation with the vectors is graphically presented. By moving the vector endpoints the vectors can be changed. The red vector is the result of the vector addition. The dotted lines are the parallel moved vectors.

⃢

↹#.000

🔍↔

🔍↕

v_x =

v_y =

w_x =

w_y =

Addition of vectors

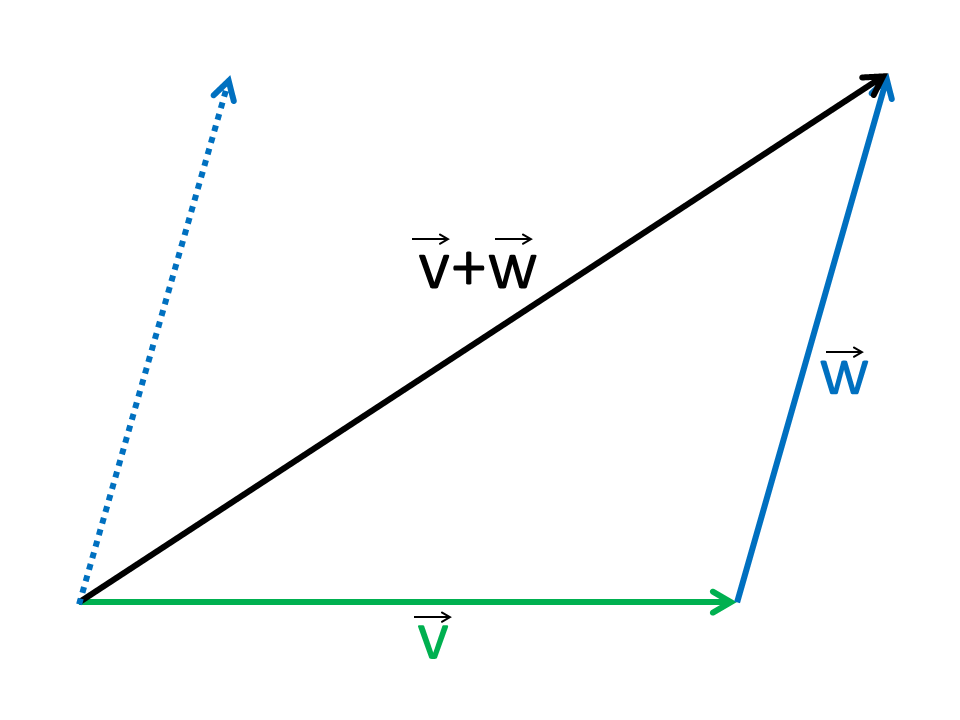
The addition of vectors is done in Cartesian coordinates componentwise. The vector addition is commutative and associative.

Geometrically, the resulting vector can be constructed by one of the vectors is parallel shifted to the other end point of the vector. The connection from the start point of the first vector to the end point of the second vector is the resultant of vector of vector addition.

$\vec{v} + \vec{w} = (\begin{matrix} v_{1} \\ v_{2} \\ ⋮ \\ v_{n} \end{matrix}) + (\begin{matrix} w_{1} \\ w_{2} \\ ⋮ \\ w_{n} \end{matrix}) = (\begin{matrix} v_{1} + w_{1} \\ v_{2} + w_{2} \\ ⋮ \\ v_{n} + w_{n} \end{matrix})$

Screenshot of the Image

Print or save the image via right mouse click.

More Calculators

Here is a list of of further useful calculators:

Vector calculation Vector subtraction Matrix-Vector product Inner product Complex numbers graphical Addition complex numbers graphical Multiplication complex numbers graphical Division complex numbers graphical Power complex numbers graphical