Vector Calculus

History of vector calculation:

The vector calculus goes back to H. G. Grassmann and parallel to Hamilton. Grassmann published in 1844 the "Lineale Ausdehnungslehre". As a precursor Descartes and Möbius apply. The Irish mathematician William Rowan Hamilton (1805 - 1865) developed the theory of quaternions, which are considered as precursors of the vectors. The term scalar goes back to Hamilton. 1888 the Italian mathematician Giuseppe Peano (1858-1932) developed an axiomatic definition of a vector space.

Scalar:

Quantities that can be represented by a real number. Examples for scalar values are temperature, mass, ...

Vector:

Vectors, in addition to its value require the specification of a direction. In physics, e.g. Velocity, field strength, ... In general, a vector is not limited to three dimensions. In general it is an n-tuple of real numbers that is often listed as a column vector.

$\vec{v} = (\begin{matrix} v_{1} \\ v_{2} \\ ⋮ \\ v_{n} \end{matrix})$

Linear Dependence:

Two vectors are called linearly dependent or collinear if one can be converted by multiplication by a scalar in the other. The cross product of collinear vectors disappears.

Orthogonality:

Two vectors are called orthogonal if the dot product of two vectors vanishes. Geometrically, the vectors are perpendicular to each other then that is the angle enclosed by the vectors is 90°.

Unit vector:

Vectors of length 1 are called unit vectors. Each vector can be converted by normalizing into the unit vector by the vector is divided by its length.

Calculation rules for vectors

Multiplication of a vector with a scalar

The multiplication of a vector by a scalar positive λ only changes the length of the vector and not direction. In the multiplication with a negative scalar, the direction of the vector changes in the opposite direction.

$λ \cdot \vec{v} = (\begin{matrix} λ \cdot v_{1} \\ λ \cdot v_{2} \\ ⋮ \\ λ \cdot v_{n} \end{matrix})$

For the multiplication of a vector by a scalar λ the distributive law holds.

$λ \cdot (\vec{v} + \vec{w}) = λ \cdot \vec{v} + λ \cdot \vec{w}$

Addition of vectors

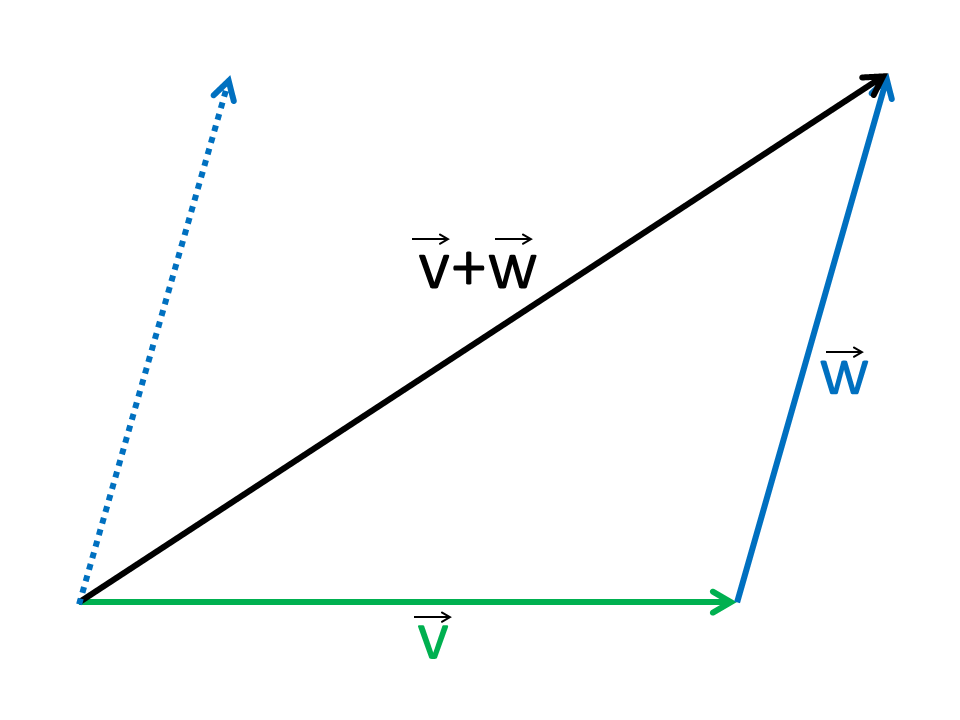
Vectors are added component by component in Cartesian coordinates. The vector addition is commutative and associative.

Geometrically, the resulting vector can be constructed by shifting one of the vectors in parallel to the endpoint of the other vector. The connection from the starting point of the first vector to the end point of the second vector is the resulting vector of the vector addition.

$\vec{v} + \vec{w} = (\begin{matrix} v_{1} \\ v_{2} \\ ⋮ \\ v_{n} \end{matrix}) + (\begin{matrix} w_{1} \\ w_{2} \\ ⋮ \\ w_{n} \end{matrix}) = (\begin{matrix} v_{1} + w_{1} \\ v_{2} + w_{2} \\ ⋮ \\ v_{n} + w_{n} \end{matrix})$

Subtraction of vectors

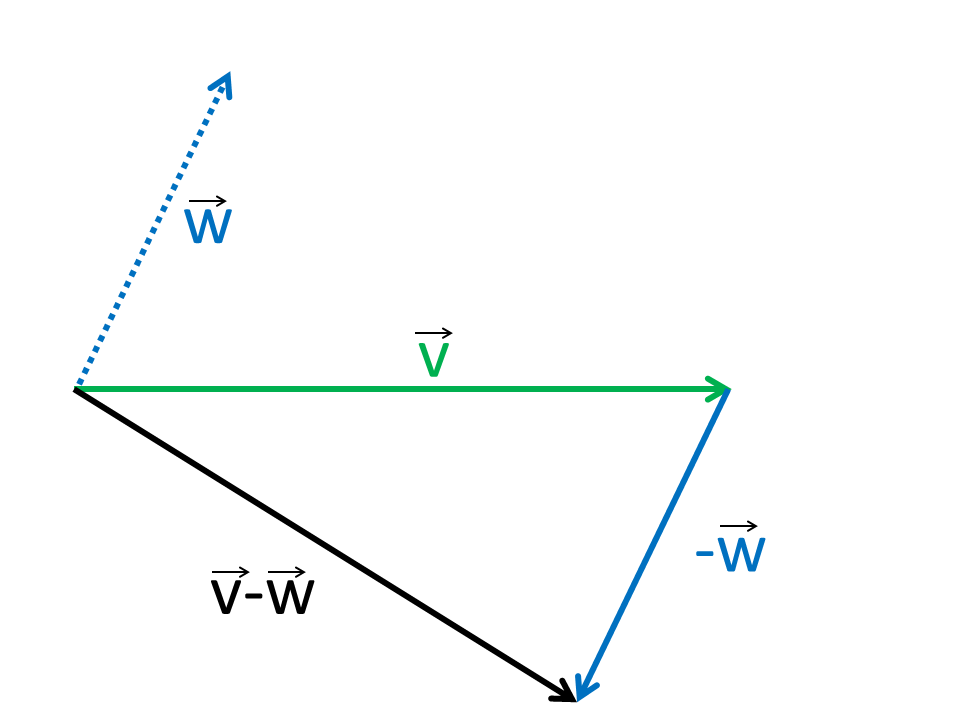
Subtraction of vectors is carried out as by the addition but the components will be subtracted.

Geometrically, the construction similar to the addition only the second vector will be mirrored to the opposite direction.

$\vec{v} - \vec{w} = (\begin{matrix} v_{1} \\ v_{2} \\ ⋮ \\ v_{n} \end{matrix}) - (\begin{matrix} w_{1} \\ w_{2} \\ ⋮ \\ w_{n} \end{matrix}) = (\begin{matrix} v_{1} - w_{1} \\ v_{2} - w_{2} \\ ⋮ \\ v_{n} - w_{n} \end{matrix})$

Dot Product (inner Product, scalar Product) of vectors

The scalar product is defined as the product of the components and the sum of these products. The scalar product is not dependent on the sequence (commutative). The name scalar product comes from the fact that the result is a scalar and not a vector.

The scalar product can be interpreted geometrically as the product of the projection of one vector in the direction of the other vector. Physically this means that the product is formed only with the component of the vector that is effective in the direction of the other vector. The scalar product can also be expressed geometrically. φ is the angle enclosed by the vectors.

$\vec{v} \cdot \vec{w} = (\begin{matrix} v_{1} \\ v_{2} \\ ⋮ \\ v_{n} \end{matrix}) \cdot (\begin{matrix} w_{1} \\ w_{2} \\ ⋮ \\ w_{n} \end{matrix}) = v_{1} \cdot w_{1} + v_{2} \cdot w_{2} + \dots + v_{n} \cdot w_{n} = \sum_{i = 1}^{n} (v_{i} \cdot w_{i})$

$\vec{v} \cdot \vec{w} = | \vec{v} | | \vec{w} | \cos φ$

For the scalar product of the distributive law apply

$\vec{u} \cdot (\vec{v} + \vec{w}) = \vec{u} \cdot \vec{v} + \vec{u} \cdot \vec{w}$

and the commutative law

$\vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{v}$

Length of a vector

The magnitude (amount) of a vector geometrically corresponds to the length of the vector.

$| \vec{v} | = | (\begin{matrix} v_{1} \\ v_{2} \\ ⋮ \\ v_{n} \end{matrix}) |$ $= \sqrt{v_{1}^{2} + v_{2}^{2} + \dots + v_{n}^{2}}$ $= \sqrt{\sum_{i = 1}^{n} v_{i}^{2}}$

Cross Product (outer Product, vector Product) of vectors

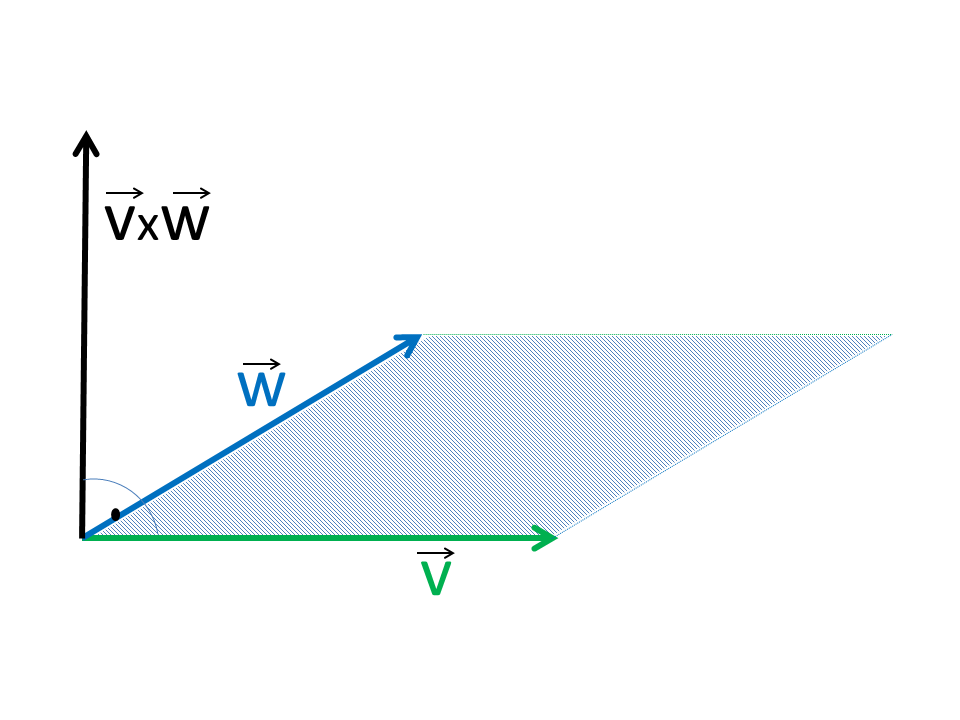
The vector product is defined in three-dimensional Euclidean vector space.

The result of the vector product is a vector which is perpendicular to the area spanned by the two vectors and whose length corresponds to the area of the parallelogram. The vector product can also be expressed geometrically. φ is the angle enclosed by the vectors and n the vector perpendicular to the surface.

$\vec{v} ⨯ \vec{w} = (\begin{matrix} v_{1} \\ v_{2} \\ v_{3} \end{matrix}) ⨯ (\begin{matrix} w_{1} \\ w_{2} \\ w_{3} \end{matrix}) = (\begin{matrix} v_{2} w_{3} - v_{3} w_{2} \\ v_{1} w_{3} - v_{3} w_{1} \\ v_{1} w_{2} - v_{2} w_{1} \end{matrix})$

$\vec{v} ⨯ \vec{w} = | \vec{v} | | \vec{w} | \sin φ \vec{n}$

The vector product is anti-commutative

$\vec{v} ⨯ \vec{w} = - (\vec{w} ⨯ \vec{v})$

Multiplication of a vector with a matrix

The product of a matrix with a vector is a linear image. The multiplication is explained if the number of columns of the matrix is equal to the number of elements of the vector. The result is a vector whose number of components equals the number of rows of the matrix. This means that a matrix with 2 rows always maps a vector to a vector with two components.

$A \cdot \vec{v} = (\begin{matrix} a_{11} & a_{12} & \dots & a_{1 m} \\ a_{21} & a_{22} & \dots & a_{2 m} \\ ⋮ \\ a_{n 1} & a_{n 2} & \dots & a_{n m} \end{matrix}) \cdot (\begin{matrix} v_{1} \\ v_{2} \\ ⋮ \\ v_{m} \end{matrix}) = (\begin{matrix} a_{11} v_{1} + a_{12} v_{2} + \dots + a_{1 m} v_{m} \\ a_{21} v_{1} + a_{22} v_{2} + \dots + a_{2 m} v_{m} \\ ⋮ \\ a_{n 1} v_{1} + a_{n 2} v_{2} + \dots + a_{n m} v_{m} \end{matrix})$

Multiple products

Multiple products of vectors are not associative in general. That the general rule is that the order in which the products are carried out is relevant.

In general is:

$\vec{u} \cdot (\vec{v} \cdot \vec{w}) \neq (\vec{u} \cdot \vec{v}) \cdot \vec{w}$

and

$\vec{u} ⨯ (\vec{v} ⨯ \vec{w}) \neq (\vec{u} ⨯ \vec{v}) ⨯ \vec{w}$

For the double vector product the development applies:

$\vec{u} ⨯ (\vec{v} ⨯ \vec{w}) = \vec{v} \cdot (\vec{u} \cdot \vec{w}) - \vec{w} \cdot (\vec{u} \cdot \vec{v})$

The scalar triple product $(\vec{u} ⨯ \vec{v}) \cdot \vec{w}$ is equal to the volume of the plane defined by the three vectors parallelepiped. The scalar triple product is positive if the three vectors form a right hand system.

Lagrange's identity:

$(\vec{m} ⨯ \vec{u}) \cdot (\vec{v} ⨯ \vec{w})$ $= (\vec{m} \cdot \vec{v}) (\vec{u} \cdot \vec{w}) - (\vec{u} \cdot \vec{v}) (\vec{m} \cdot \vec{w})$

Geometrical approches

Equation of the line through the two points P₀ und P₁ given by the vectors r₀ und r₁:

$\vec{r} = \vec{r_{0}} + λ (\vec{r_{1}} - \vec{r_{0}})$

Distance of two points P₀ and P₁:

$| \vec{r_{1}} - \vec{r_{0}} |$