Online calculator for Fourier series expansion

Calculator for Fourier series expansion to any measured values or functions

A Fourier series, after Joseph Fourier (1768-1830), is the series expansion of a periodic, sectionally continuous function into a function series of sine and cosine functions.

The calculator can be used to perform a Fourier series expansion on any measured value or, alternatively, on a function.

⃢

↹#.000

🔍↔

🔍↕

Fourier series:

Number of Fourier components:

Modes:

Offset

Stretch

f(x):

Interval

min=

max=

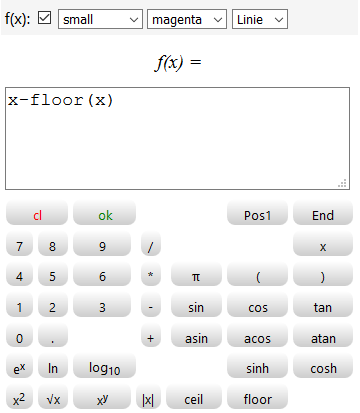
f(x)=

Pos1

End

(

)

sin

cos

tan

e^x

1/x

asin

acos

atan

x²

√x

ceil

floor

|x|

sinh

cosh

\sin (π x + \frac{π}{4})

\cos (π x + \frac{π}{4})

\tan (π x + \frac{π}{4})

\sin^{2} (π x + \frac{π}{4})

\cos^{2} (π x + \frac{π}{4})

\tan^{2} (π x + \frac{π}{4})

\frac{1}{\sin (x)}

\frac{1}{\cos (x)}

\frac{1}{\tan (x)}

\frac{\sin (x)}{\cos (π \cdot x)}

\sin (\cos (x))

e^{x} \sin (x) \cos (x)

^x+1 / _x+2

^x²-1/ _x²+1

¹ / _x+1

^1+√x / _1-√y

√x+1

√e^x

x²+x+1

With the Fourier expansion of a function the integration range can be specified (interval). When points are specified, linear interpolation is performed between the points and the integration range extends from the first to the last specified point.

Function	Description
sin(x)	Sine of x
cos(x)	Cosine of x
tan(x)	Tangent of x
asin(x)	arcsine
acos(x)	arccosine of x
atan(x)	arctangent of x
atan2(y, x)	Returns the arctangent of the quotient of its arguments.
cosh(x)	Hyperbolic cosine of x
sinh(x)	Hyperbolic sine of x
pow(a, b)	Power a^b
sqrt(x)	Square root of x
exp(x)	e-function
log(x), ln(x)	Natural logarithm
log(x, b)	Logarithm to base b
log2(x), lb(x)	Logarithm to base 2
log10(x), ld(x)	Logarithm to base 10

more ...

Points:

Polygon:

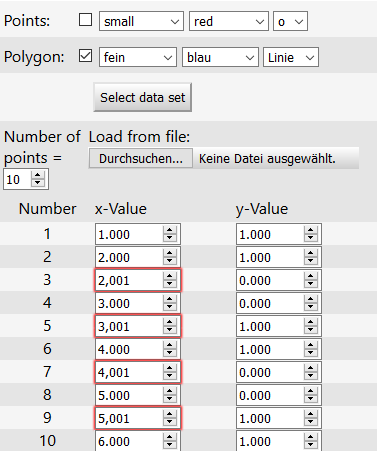
An alternative input is possible with load data from file. The values may be separated comma or space or semicolon. The values must be given pairwise x₁,y₁,x₂,y₂...

Fourier coefficients:

Fourier Series

Measured values and functions can be approximated by the periodic functions. The procedure for this is the development of a Fourier series. The elements of the Fourier series are sine and cosine functions. The development takes place in ascending order of frequencies.

The Fourier series is:

$s_{n} (x) = \frac{a_{0}}{2} + \sum_{k = 1}^{n} (a_{k} cos (k ω x) + b_{k} sin (k ω x))$

with the Fourier coefficients a_k und b_k and ω = 2π/T. This is the period T = b - a with the initial interval a and the end of interval b.

The Fourier coefficients a_k und b_k satisfy the least squares condition for the associated sine or cosine function. The coefficients are calculated as follows.

$a_{k} = \frac{2}{l} \int_{a}^{b} f (x) cos (k ω x) dx$

$b_{k} = \frac{2}{l} \int_{a}^{b} f (x) sin (k ω x) dx$

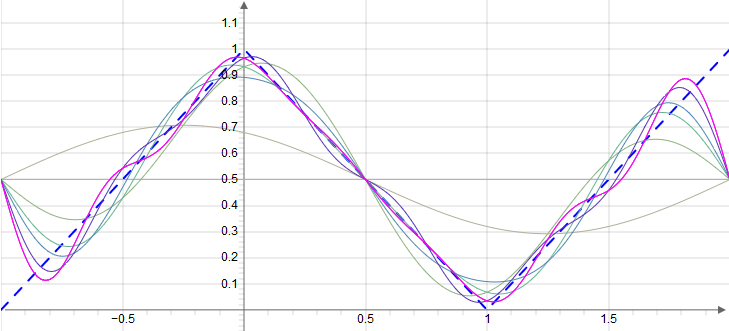
Example: Sawtooth function

Example: Triangle function

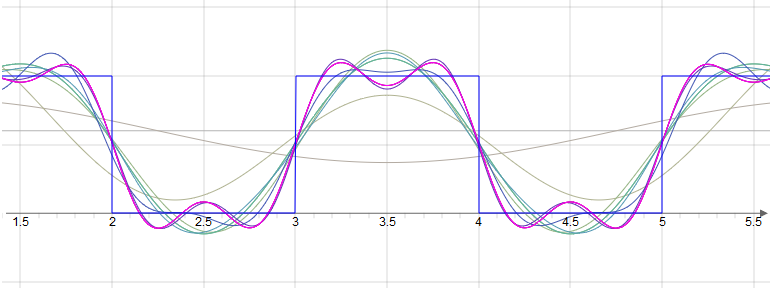
Example: Rectangle function

Screenshot of the logistc growth graph

Print or save the image via right mouse click.

Releated sites

Here is a list of of further useful sites:

Index Online Fourier Transform Calculator Curve fitting for: linear line, power function, polynomial, normal distribution Newton Interpolation Horners Method Trigonometric calculations Taylor series calculator Normal Distribution Plot NxN Gauss method Derivation rules ODE first order