Stepwise polynomial division with the Horner scheme
To perform the polynomial division with the Horner scheme, first the polynomial coefficients are transferred to the scheme. The coefficients of the first polynomial are entered in the first line of the scheme. For missing elements of the polynomial a 0 is entered. The coefficients of the second polynomial form the first column of the scheme. It should be noted that the coefficients are multiplied by -1. The following figure shows an example of the structure of the Horner scheme.
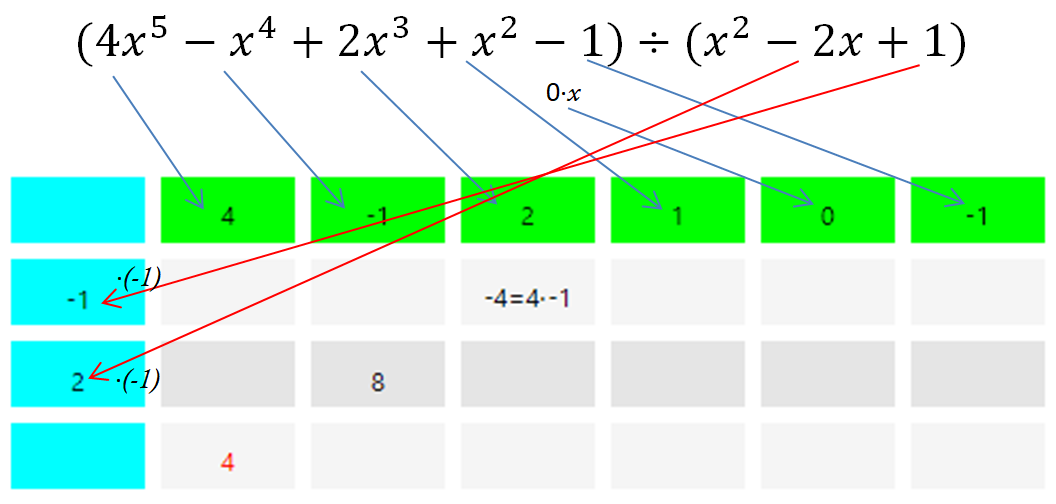
In the next step, the sum is formed over the first column and the result is entered in the bottom row of the schema. This value is now multiplied by the elements of the first column and entered into the schema in each case.
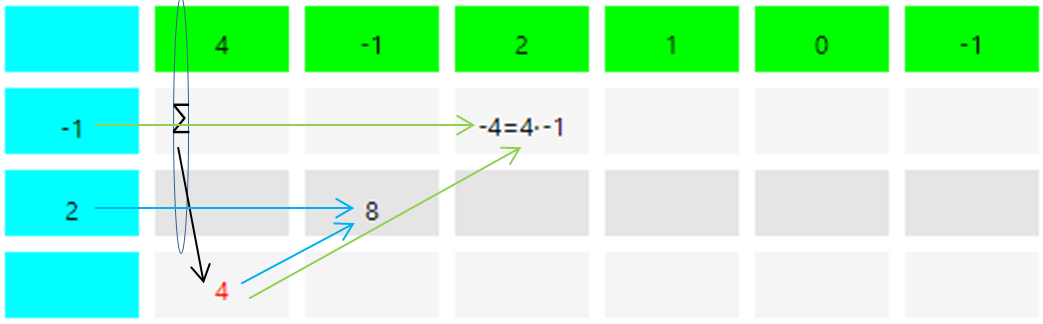
The rest of the procedure is analogous. First the sum the next column formed and the result into the lowest line of the scheme enter. Multiply this value with the elements of the first column and enter each in the scheme.
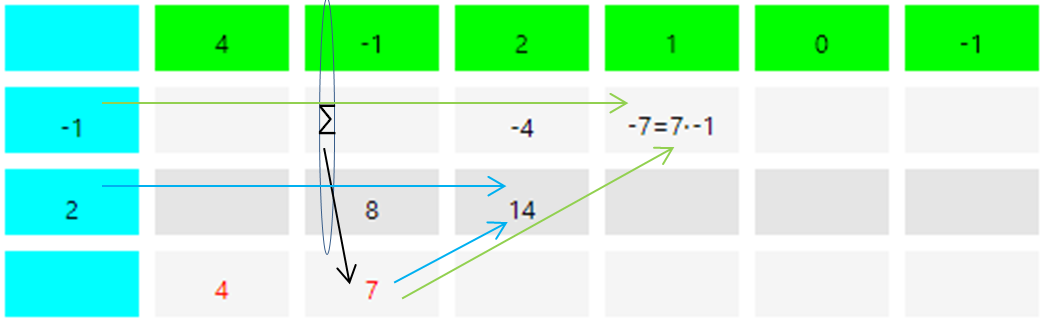
Continue in this way until the end of the scheme is reached. Then the coefficients of the result of the polynomial division can be read in the lowest line of the Horner scheme.
