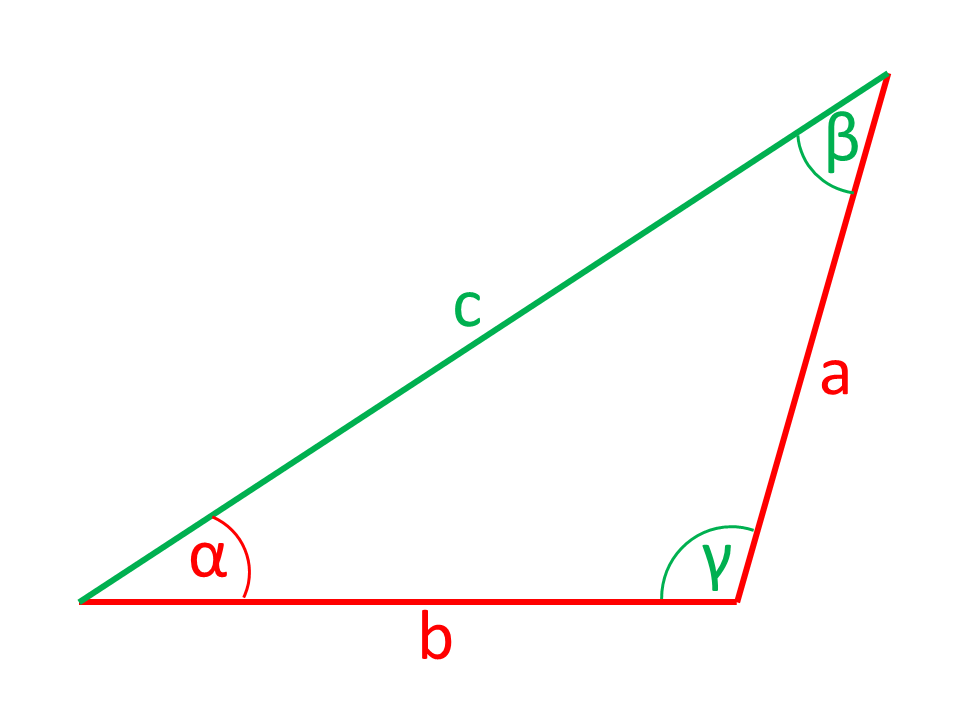
Online calculator trigonometry

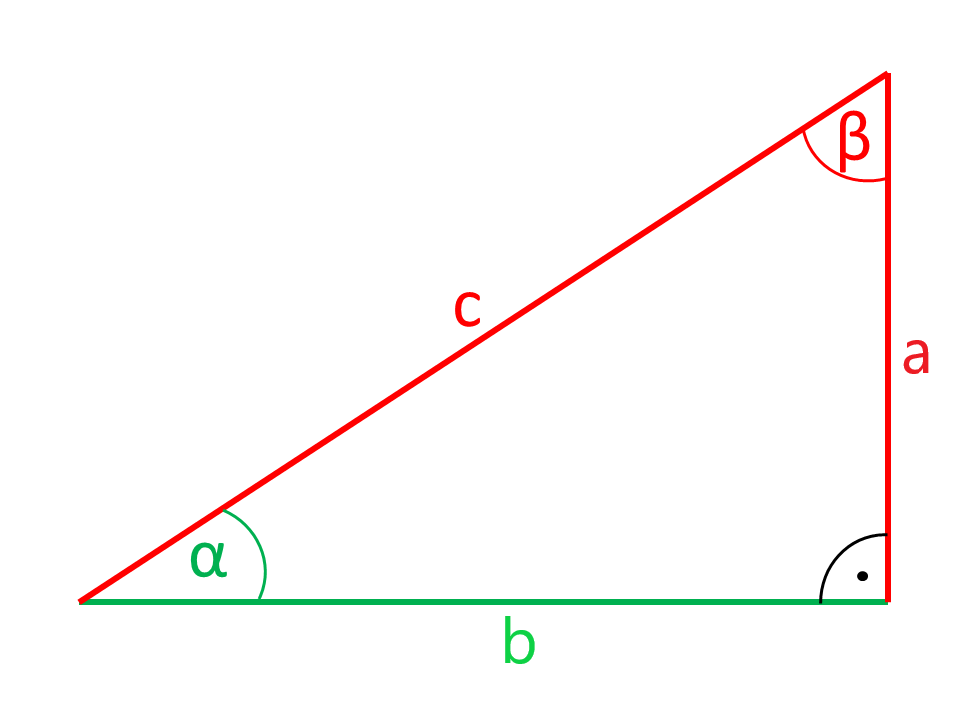
Calculator for rectangular triangle

The sides or angles are shown in the illustrations in red color are calculated by the calculator from the sides and angles shown in green color.

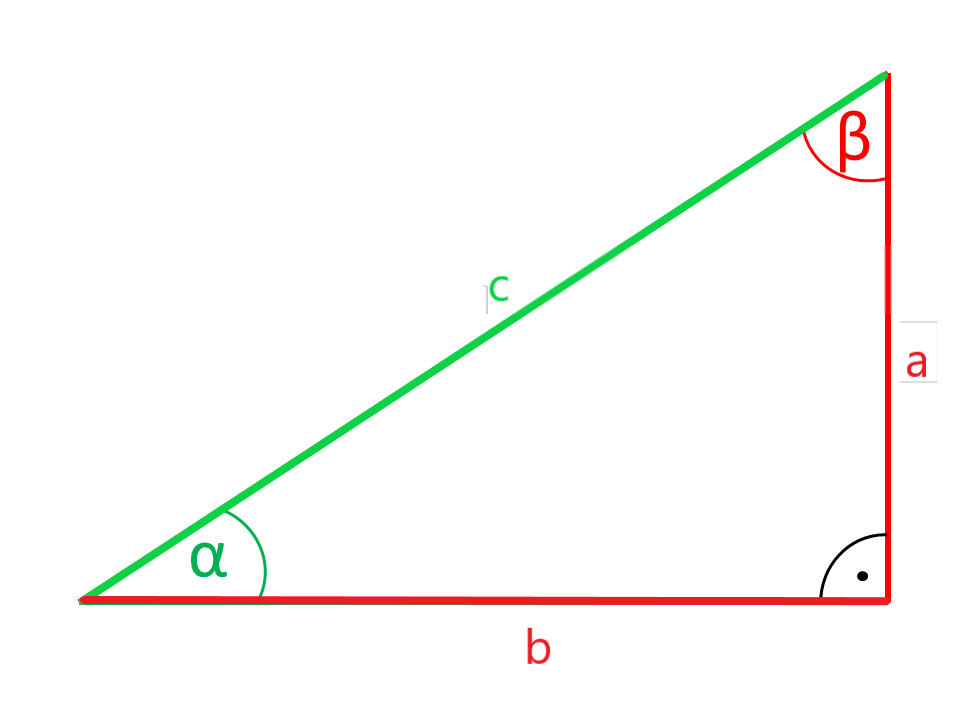
Angle and opposite cathetus

α in degree =

a =

Angle and adjacent cathetus

α in degree =

b =

Angle and hypotenuse

α in degree =

c =

Cathetus

a =

b =

Cathetus and hypotenuse

b =

c =

Calculator for general triangles

Two sides and one angle

γ in degree =

a =

b =

Two angles and one side

γ in degree =

β in degree =

c =

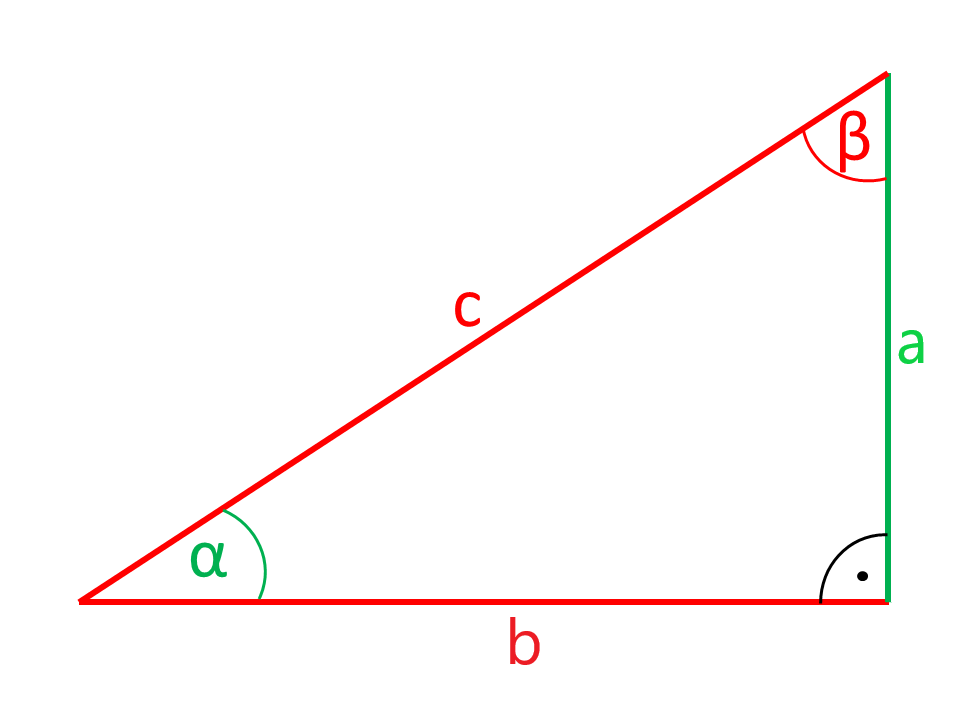
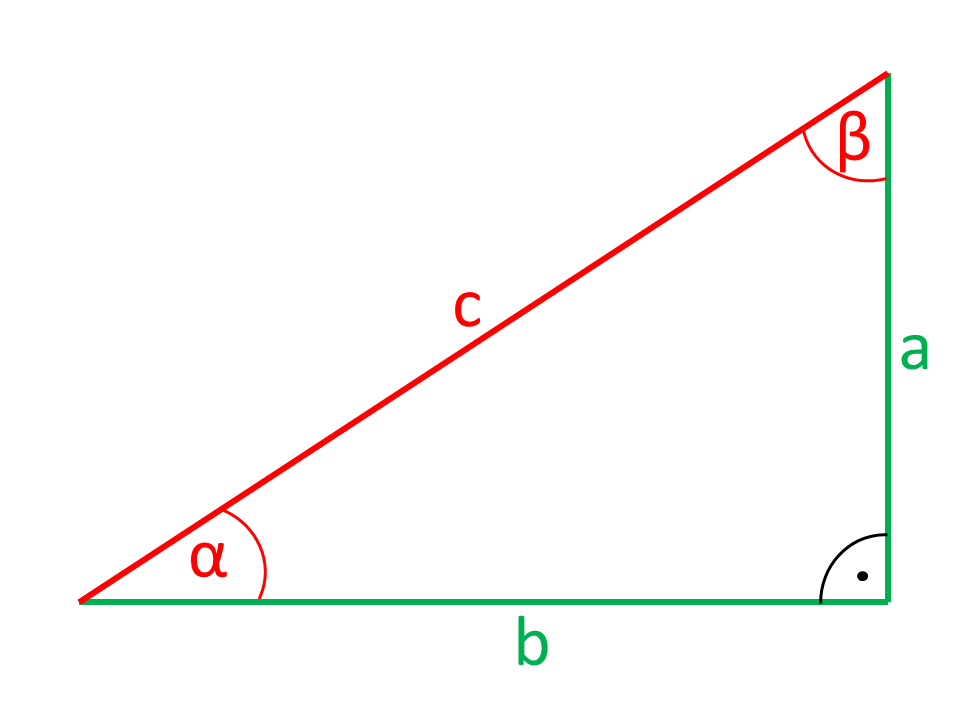
Three sides

a =

b =

c =

Examples of trigonometric calculations

Here are some examples that illustrate the application of trigonometric formulas.

Example: Calculation of tower height

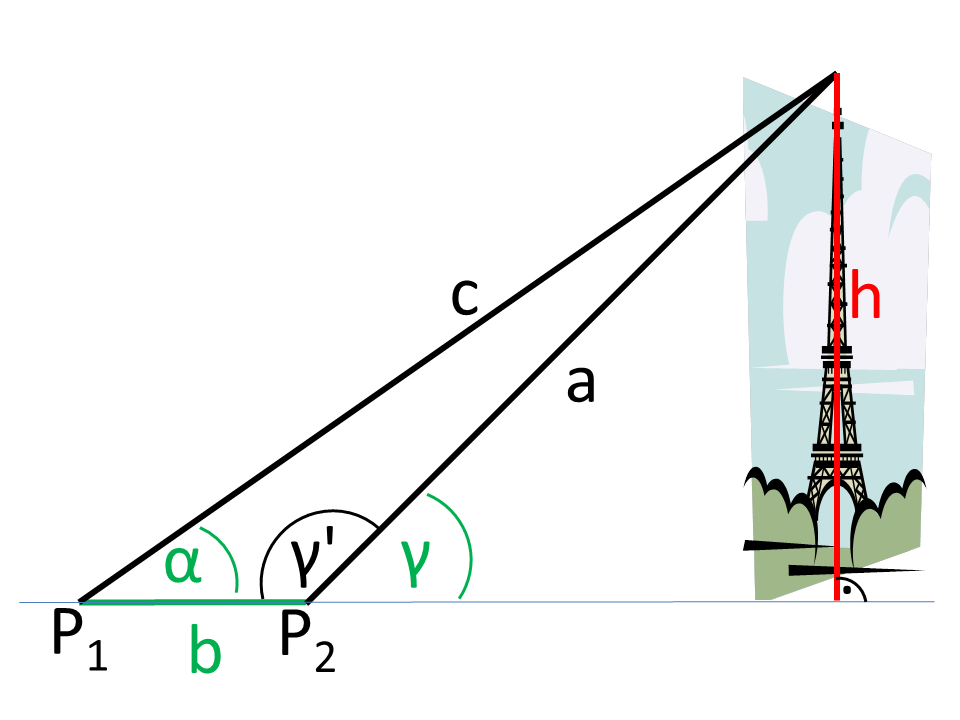
The example shows how a height can be determined, even if direct access is not possible.

The figure shows that the viewing angles (α, γ) and the distance b of the positions were determined from two positions (P₁, P₂) (green in the Illustration).

A triangle is formed from P₁, P₂, and the tower tip. From this general triangle, the angle α and the side b is known. The angle γ can be calculated as follows:

$\mathrm{\gamma \text{'}}=180-\mathrm{\gamma }$

The still missing angle β can be determined, since the angular sum in the triangle is 180°.

$\beta =180-\mathrm{\alpha }-\mathrm{\gamma \text{'}}=\mathrm{\gamma }-\mathrm{\alpha }$

In the next step, the sinus set is used to calculate the side a. The side a is a common side of the general triangle and the right-angled triangle formed by a and the height of the tower and the base line.

$a=\sin \left(\alpha \right)\frac{b}{\sin \left(\beta \right)}=b\frac{\sin \left(\alpha \right)}{\sin \left(\gamma -\alpha \right)}$

In the right-angled triangle, a is the hypotenuse, and h is the opposite leg of the angle γ. The desired height h can thus be calculated with the angular function.

$h=a\sin \left(\gamma \right)=b\frac{\sin \left(\alpha \right)\sin \left(\gamma \right)}{\sin \left(\gamma -\alpha \right)}$

Alternatively, the tower height can also be calculated by applying two equations for the right-angled triangle. The first triangle is made up of P₁ and the base of the tower as well as the tower tip. The second analogous outgoing of P₂.

It is:

$\tan \gamma =\frac{h}{x}$

and

$\tan \alpha =\frac{h}{b+x}$

with the unknown distance x from P₂ to the base point of the tower.

Reshaping the equations results in each case:

$x=\frac{h}{\tan \gamma }$

and

$x=\frac{h-b\tan \alpha }{\tan \alpha }$

Equating the equations and solving for h yields the solution:

$h=b\frac{\tan \alpha \tan \gamma }{\tan \gamma -\tan \alpha }$

The two solutions for h are equivalent can be easily proved with replacing of

$\tan \left(\alpha \right)=\frac{\sin \left(\alpha \right)}{\cos \left(\alpha \right)}$

and

$\tan \left(\gamma \right)=\frac{\sin \left(\gamma \right)}{\cos \left(\gamma \right)}$

$h=b\frac{\tan \alpha \tan \gamma }{\tan \gamma -\tan \alpha }=b\frac{\sin \alpha \sin \gamma }{\sin \gamma \cos \alpha -\sin \alpha \cos \gamma }$

With addition theorem

$\sin \left(x\pm y\right)=\sin \left(x\right)\cos \left(y\right)\pm \cos \left(x\right)\sin \left(y\right)$

the above solution results.

It is

$h=b\frac{\tan \alpha \tan \gamma }{\tan \gamma -\tan \alpha }=b\frac{\sin \left(\alpha \right)\sin \left(\gamma \right)}{\sin \left(\gamma -\alpha \right)}$

Example: Cross bearing

A fixed point (for example, a lighthouse) from two positions is targeted at the cross-bearing. A constant course and a constant speed are applied between the two bearings (P₁, P₂). Then the distance from the target point can be determined from the bearings.

The figure shows that the viewing angles (α, γ) relative to the direction of travel were determined at two positions (P₁, P₂) (green in the figure). The side length b is obtained from the velocity v and the time interval t of the measurements.

A triangle is formed from P₁, P₂ and the target point (lighthouse). From this general triangle, the angle α and the side b = v * t is known.

The still missing angle β can be determined, since the angular sum in the triangle is 180°.

$\beta =180-\mathrm{\alpha }-\mathrm{\gamma }$

In the next step, the sine rule is used to calculate the side a. The side a is the distance from the measuring point P₁.

$a=\sin \left(\alpha \right)\frac{b}{\sin \left(\beta \right)}$

The distance to the second measuring point is calculated analogously.

$c=\sin \left(\gamma \right)\frac{a}{\sin \left(\alpha \right)}$

Example: Measurement of an inaccessible route (Hansen's task)

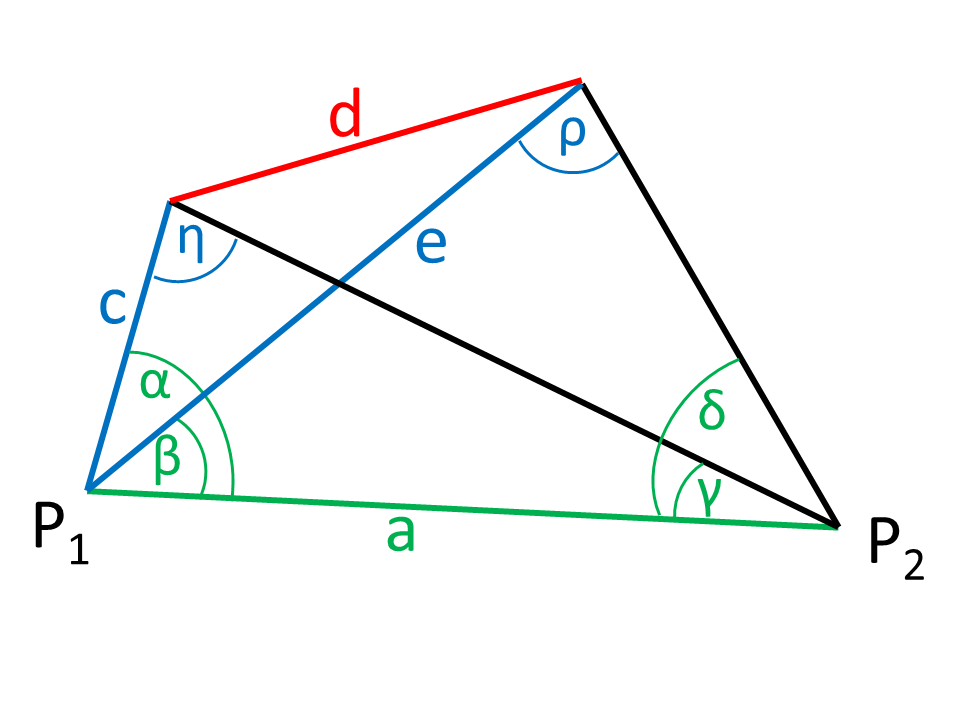
In order to measure an inaccessible route, the start and end of the route are determined from two points (P₁, P₂).

The figure shows that the angles of view (α, β, γ, δ) at two positions (P₁, P₂) relative to the connecting axis of the points (green in the figure). The distance a of the measuring points is also known. The length of the inaccessible distance d (red in the figure) is to be determined.

The figure shows the blue values to be calculated.

The angle η can be determined, since the angular sum in the triangle is 180°.

$\eta =180-\mathrm{\alpha }-\mathrm{\gamma }$

In the next step, the sine rule is used to calculate the side c.

$c=a\frac{\sin \left(\gamma \right)}{\sin \left(\eta \right)}$

The side e is also calculated with the sine rule.

$e=a\frac{\sin \left(\delta \right)}{\sin \left(\rho \right)}$

The angle ρ results from the angle sum in a triangle.

$\rho =180-\mathrm{\beta }-\mathrm{\delta }$

The cosine rule can now be used to calculate the required distance d.

$d^2=a^2+c^2-2ac\cos \left(\alpha -\beta \right)$

Example: Triangle of forces on pendulum

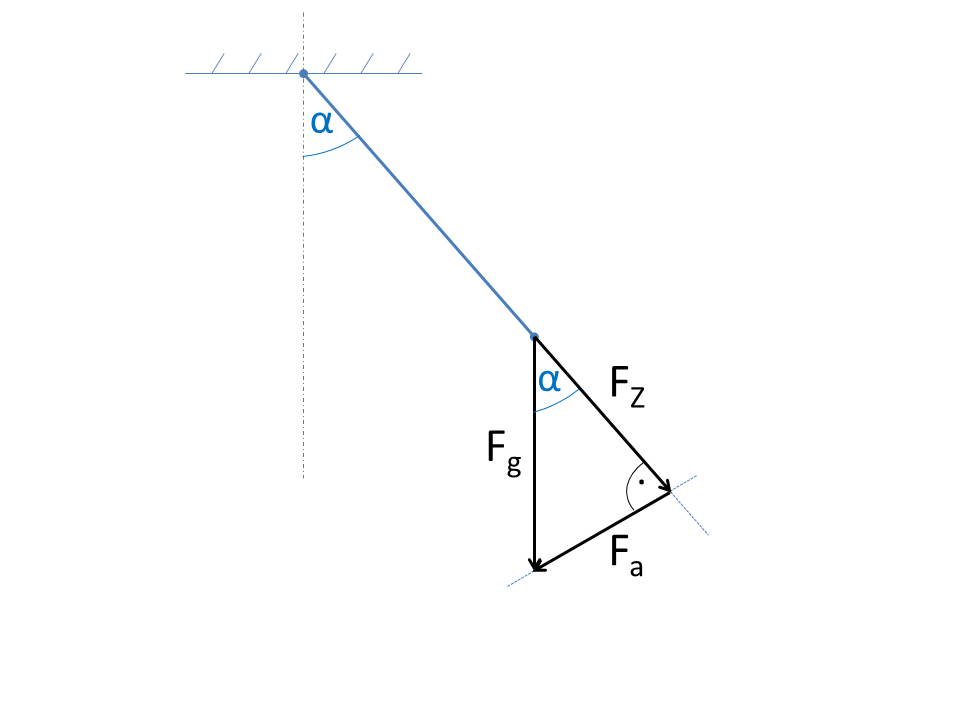
The decomposition of forces into orthogonal components plays an important role in mechanics. This example shows how the weight force can be decomposed into two components by means of the angle functions.

The figure shows a yarn pendulum with a mass at the end of the thread. The weight force F _g is to be decomposed into partial forces. The force in the direction of the thread F _Z does not contribute to the acceleration and the force F _a is therefore relevant for the motion equation.

The partial forces can be specified directly by means of the angle functions, since they are a right-angled triangle.

$F_a=F_g\sin \left(\alpha \right)$

$F_Z=F_g\cos \left(\alpha \right)$

General Trigonometry

The basic task of Trigonometry is (etc. Side lengths, angle sizes, lengths of triangle-transversal) to be calculated from three sizes of a given triangle other sizes of this triangle. As an aid to the trigonometric functions sine (sin), cosine (cos), tangent (tan), Cotangent (cot). Precursor of Trigonometry there was already during Antiquity in Greek Mathematics. Aristarchus of Samos took advantage of the properties of right triangles to calculate the distance relationships between the earth and sun and moon.

Right Angle Triangle

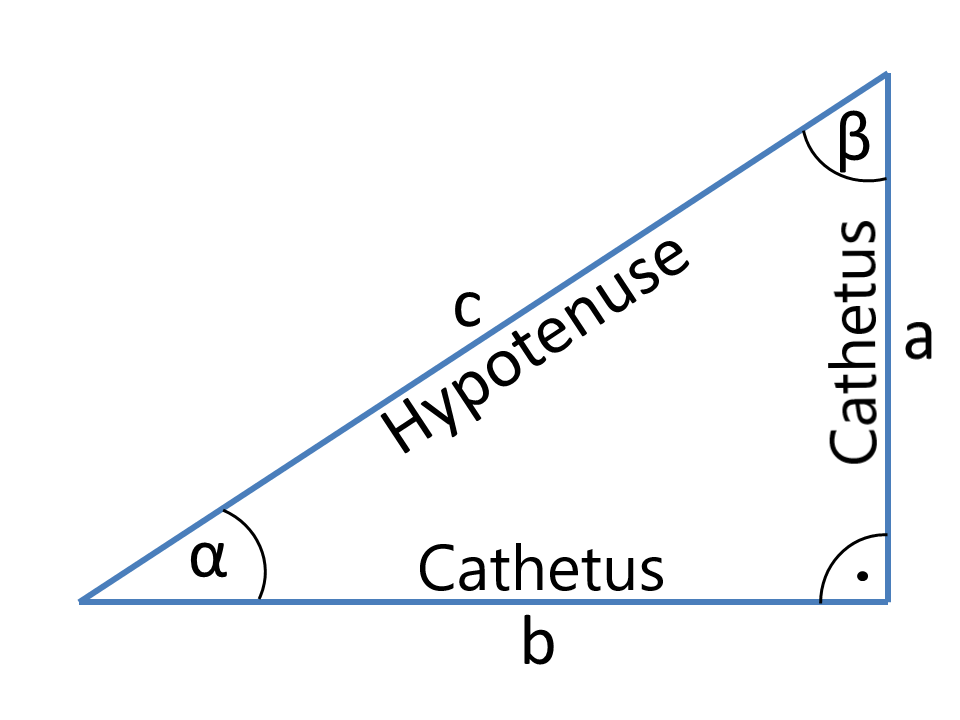
Definitions

The sides a and b of the right angle triangle, which include the right angle are the cathetus. The right angle opposite side c is the hypotenuse. Looking at the angle α as the side a is the adjacent side and the opposite side b.

Trigonometric functions

$\sin \left(\alpha \right)=\cos \left(\beta \right)=\frac{a}{c}$

$\cos \left(\alpha \right)=\sin \left(\beta \right)=\frac{b}{c}$

$\tan \left(\alpha \right)=\cot \left(\beta \right)=\frac{a}{b}$

Degree / Radians

Angle can be specified in degree (deg) or radians (rad). The full circle in degree is 360 degree in radians it is 2π. Accordingly, the following conversions apply.

$\text{Angle (rad)}=\frac{\pi }{180}\text{Angle (deg)}$

$\text{Angle (deg)}=\frac{180}{\pi }\text{Angle (rad)}$

Angle sum

The sum of the angles in a triangle is 180°. This applies in the right-angled triangle the following relationship for the angle.

$90=\alpha +\beta$

General Triangle

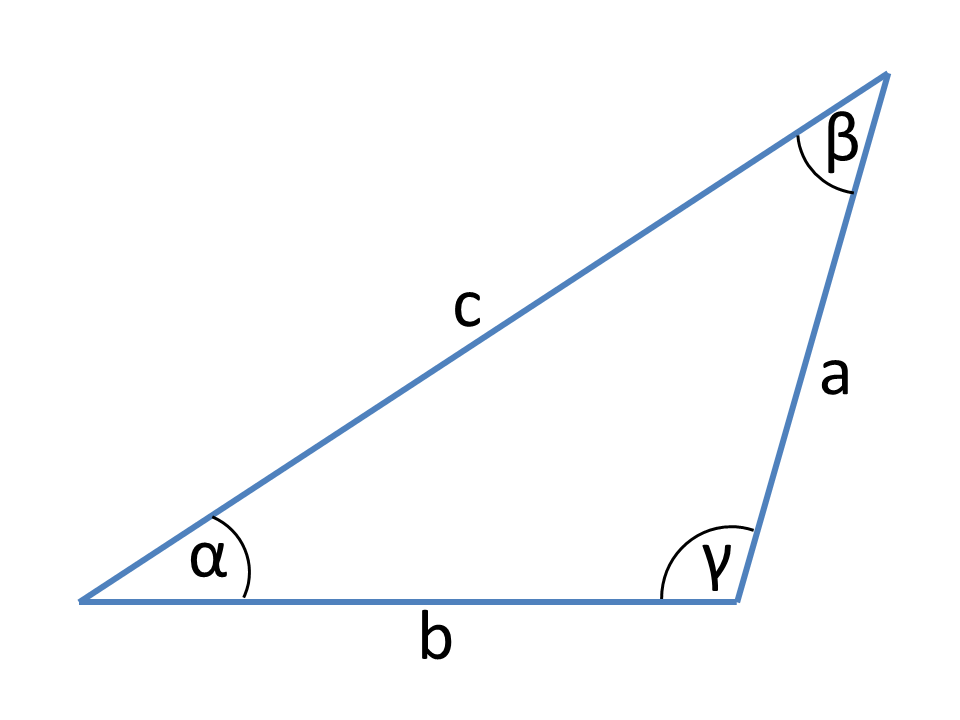
Definitions

Essential for the calculations in general triangle are the cosine and the sine law and the relationship of the trigonometric functions.

Sine law

$\frac{a}{\sin \left(\alpha \right)}=\frac{b}{\sin \left(\beta \right)}=\frac{c}{\sin \left(\gamma \right)}$

Cosine law

$a^2=b^2+c^2-2bc\cos \left(\alpha \right)$

$b^2=a^2+c^2-2ac\cos \left(\beta \right)$

$c^2=a^2+b^2-2ab\cos \left(\gamma \right)$

Projection law

$c=a\cdot \cos \left(\beta \right)+b\cdot \cos \left(\alpha \right)$

Tangent formula

$\tan \left(\gamma \right)$$=\frac{c\cdot \sin \left(\alpha \right)}{b-c\cdot \cos \left(\alpha \right)}$$=\frac{c\cdot \sin \left(\beta \right)}{a-c\cdot \cos \left(\beta \right)}$

Angle sum

The sum of the angles in a triangle beträt 180°.

$180=\alpha +\beta +\gamma$

Circumradius r

$r=\frac{s}{4\cdot \cos \left(\frac{\alpha }{2}\right)\cdot \cos \left(\frac{\beta }{2}\right)\cdot \cos \left(\frac{\gamma }{2}\right)}$

with

$s=\frac{1}{2}\left(a+b+c\right)$

Inscribed circle radius ρ

$\rho =\sqrt{\frac{\left(s-a\right)\left(s-b\right)\left(s-c\right)}{s}}$

Height h_c on c

$h_c=a\cdot \sin \left(\beta \right)=b\cdot \sin \left(\alpha \right)$

Area A

$A=\frac{1}{2}a\cdot b\cdot \sin \left(\gamma \right)$

Heronische area formula

$A=\rho s=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}$

Properties of trigonometric functions

Reducing formulas (in Degree)

$\sin \left(\mathrm{90°}+x\right)=\cos \left(x\right)$

$\cos \left(\mathrm{90°}+x\right)=-\sin \left(x\right)$

$\tan \left(\mathrm{90°}+x\right)=-\cot \left(x\right)$

$\cot \left(\mathrm{90°}+x\right)=-\tan \left(x\right)$

$\sin \left(\mathrm{180°}+x\right)=-\sin \left(x\right)$

$\cos \left(\mathrm{180°}+x\right)=-\cos \left(x\right)$

$\tan \left(\mathrm{180°}+x\right)=\tan \left(x\right)$

$\cot \left(\mathrm{180°}+x\right)=\cot \left(x\right)$

Trigonometric functions with equal arguments

${\sin \left(x\right)}^2+{\cos \left(x\right)}^2=1$

$\tan \left(x\right)=\frac{\sin \left(x\right)}{\cos \left(x\right)}$

Addition theorem of trigonometric functions

$\sin \left(x\pm y\right)=\sin \left(x\right)\cos \left(y\right)\pm \cos \left(x\right)\sin \left(y\right)$

$\cos \left(x\pm y\right)=\cos \left(x\right)\cos \left(y\right)\mp \sin \left(x\right)\sin \left(y\right)$

$\tan \left(x\pm y\right)=\frac{\tan \left(x\right)\pm \tan \left(y\right)}{1\mp \tan \left(x\right)\tan \left(y\right)}$

More Calculators

Here is a list of of further useful calculators:

Index Trigonometry Tables Sine, Cosine, Tangent Power and n-th argument Triangle Derivative sine cosine tangent