Online Ellipse Calculator
Interactive Ellipse calculator
Move the points in the grafic or define the point coordinates in the numeric field. Pulling the focal points F1, F2 and the peripherie point P allows the ellipse to be varied. The center of the ellipse is marked by the center point C The currently calculated ellipse values are shown below.
Properties of the ellipse
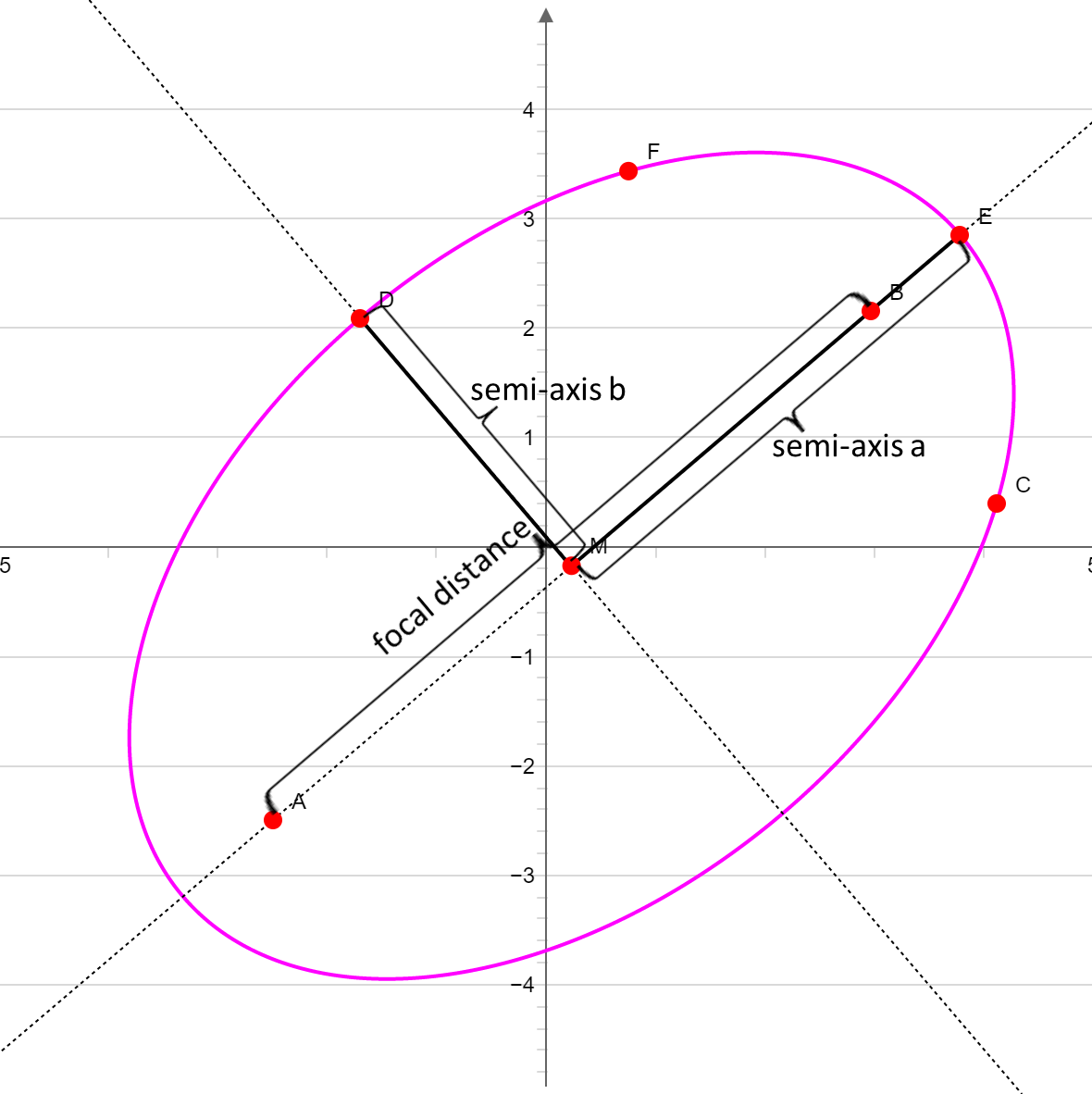
The ellipse is the set of all geometric locations for which the sum of the distances of two fixed points (A and B) is constant.
The ellipse equation in cartesian co-ordinates is given by:
with the ellipse center M at mx and my.
In parameter representation the ellipse equation is given as follows
Circumference of the ellipse
With the semiaxis a = ME and b = MD is the circumference of the ellipse given by:
with
Approximation formula for the elliptical perimeter according to Ramanujan:
Ellipse area
With the half-axes a and b the area of the ellipse is given by:
Focal distance
With the larger semi-axis a the distance of the focal points of the ellipse is given by:
Eccentricity
With the larger semi-axis a, eccentricity of the ellipse is given by:
Tangent
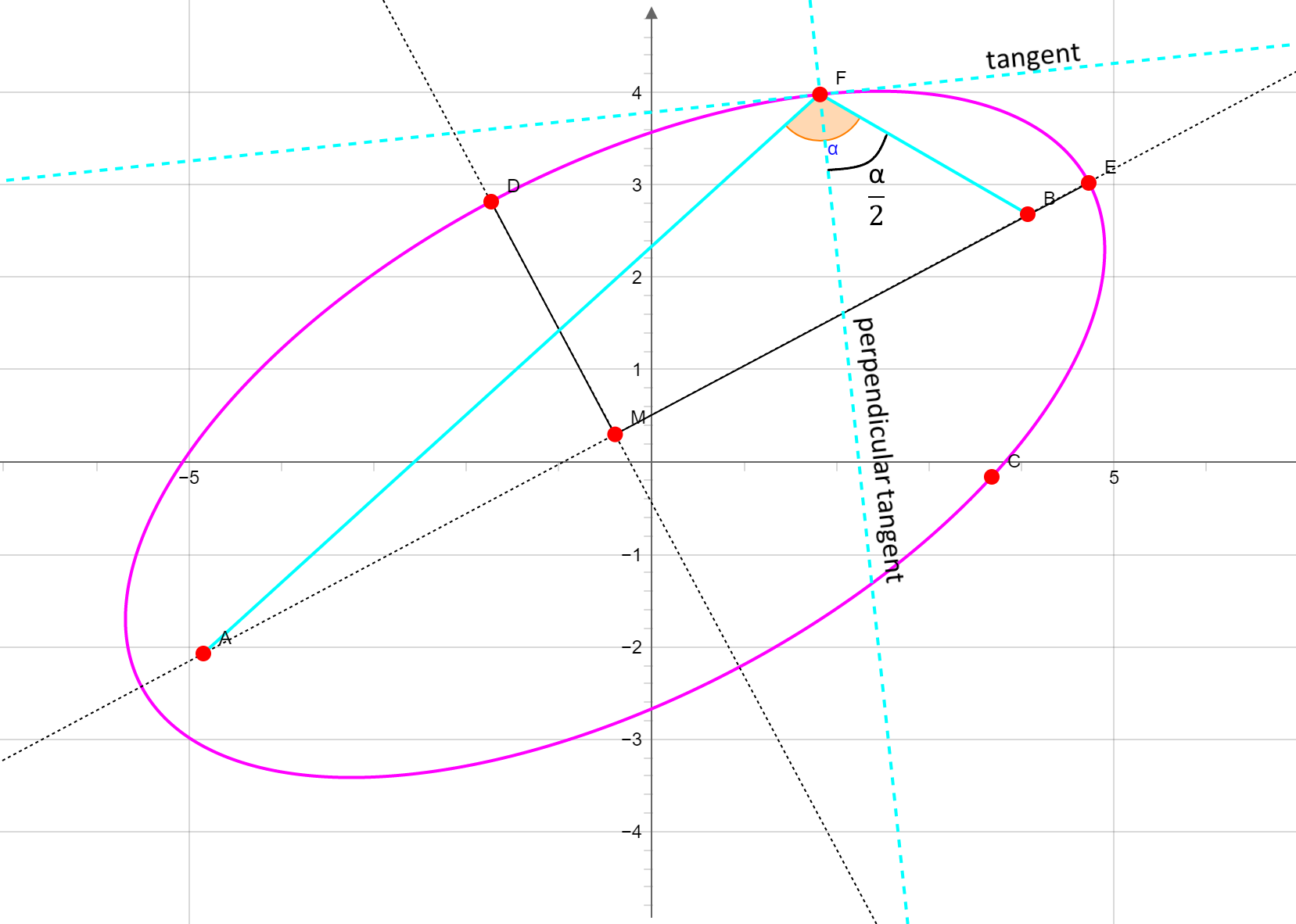
The perpendicular to the tangent of the ellipse halves the angle that the focal spot beams (AF and FB) form at the tangent point F.
Screenshot of the Image
Print or save the image via right mouse click.
Releated sites
Here is a list of of further useful sites:
Index Trigonometric calculations Circle Triangle Parallelogram Rectangle