Online Interactive Circle

Circle calculator with segment and sector calculation

Points A and B define the circle and can be changed numerically or graphically. A defines the center and B the radius. C defines the sector and segment. For the circle, the circle data radius, area and circumference are calculated. For the sector element the secant length, the opening angle and the sector area. For the segment, the arc length of the circle segment, the area of the circle segment and the height of the segment. With the cross on the radius the ring can be changed. For the ring the area and the sector section of the ring are calculated. The checkboxes allow to switch the graphic elements on and off.

⃢

↹#.000

🔍↔

🔍↕

Circle:

Radius

Circumference

Area

Sector:

Secant length

Area

Opening angle

Segment:

Arc length

Area

Height

Ring:

Width

Area

Points (x, y)

A =

B =

C =

Axis ranges

x-min=

x-max=

y-min=

y-max=

Circle:

Secant:

Sector:

Arc:

Height h_a

Points:

Ring:

Properties of the circle

Circle radius:

The radius r is the distance from the center of the circle to the circle circumference. A circle is defined by the set of all points that have the distance r to a point.

Circle diameter:

The circle diameter d is the straight line that connects two different points of the circle periphery and passes through the circle center.

$d = 2 r$

Circle circumference:

$U = 2 π r = π d$

Circle area:

$F = π r^{2}$

Circle secant (chord)

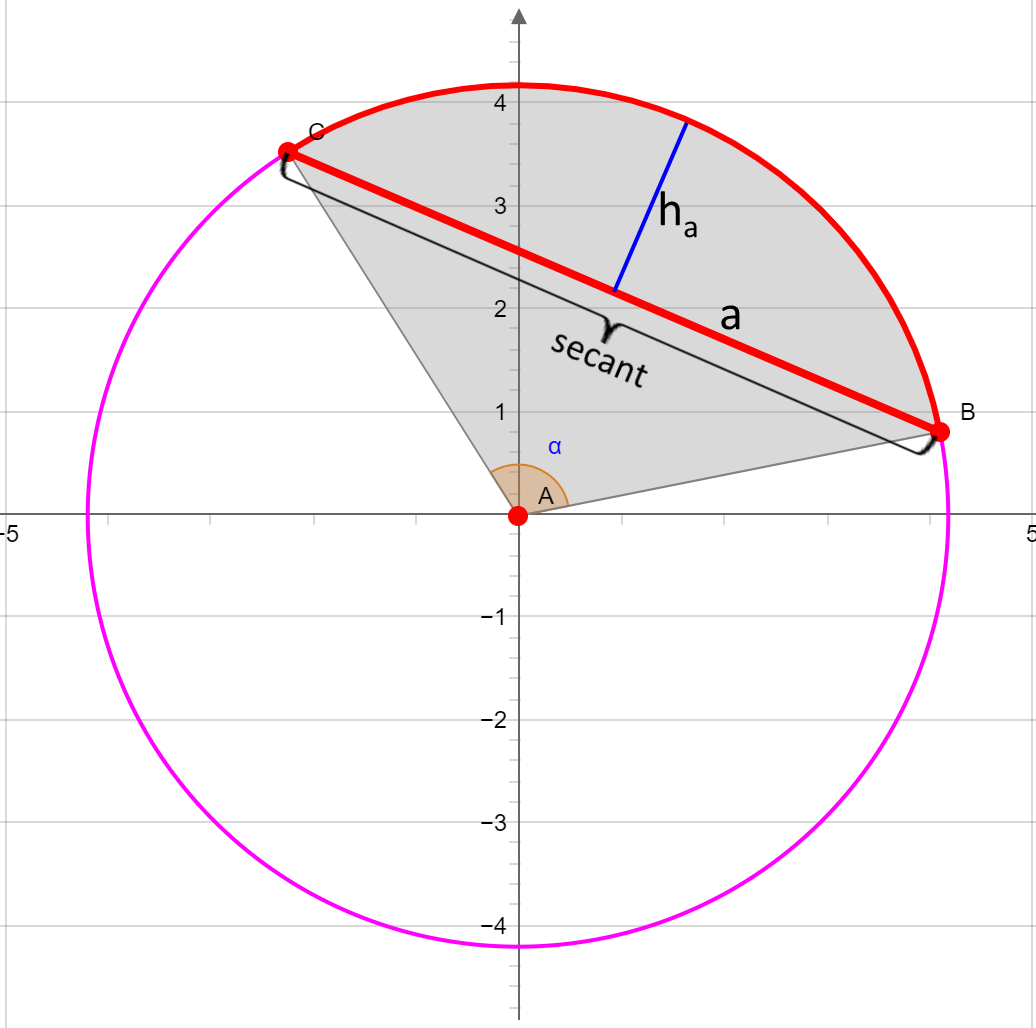
The chord or secant connects two points of the circle circumference. The length of the secant a is:

$a = 2 r \sin (\frac{α}{2}) = 2 \sqrt{2 h_{a} r - {h_{a}}^{2}}$

with the opening angle α of the sector and the height h_a of the circular section.

Arc length

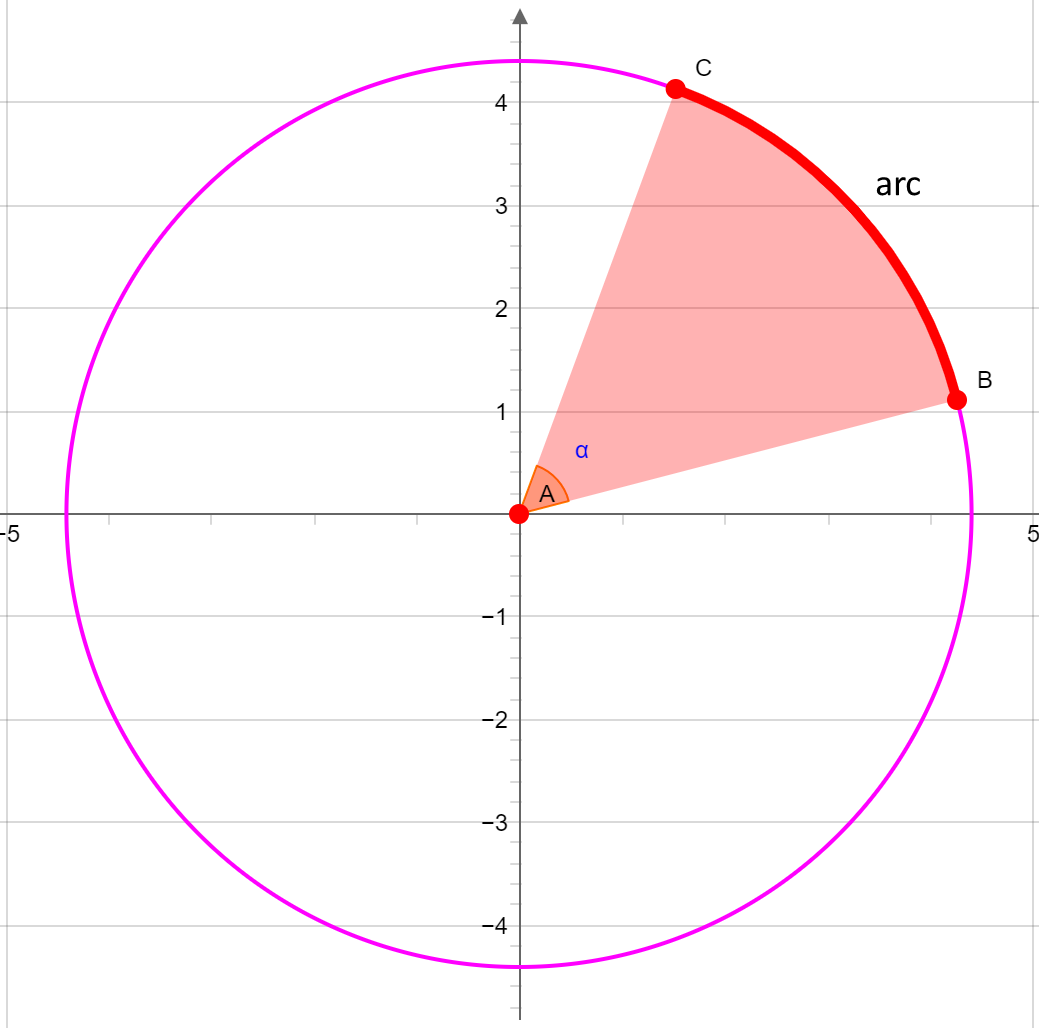
The arc length l of the segment (arc between B and C) with the opening angle α of the sector in degree is:

$l = 2 π r \frac{α}{360°}$

With the angle in radians is:

$l = 2 π r \frac{α}{2 π}$

Sector area

The colored area shows a circular sector of the circle. The area S of the circular sector with the angle in degree is:

$S = π r^{2} \frac{α}{360°}$

With the angle in radians is:

$S = π r^{2} \frac{α}{2 π}$

Circular segment

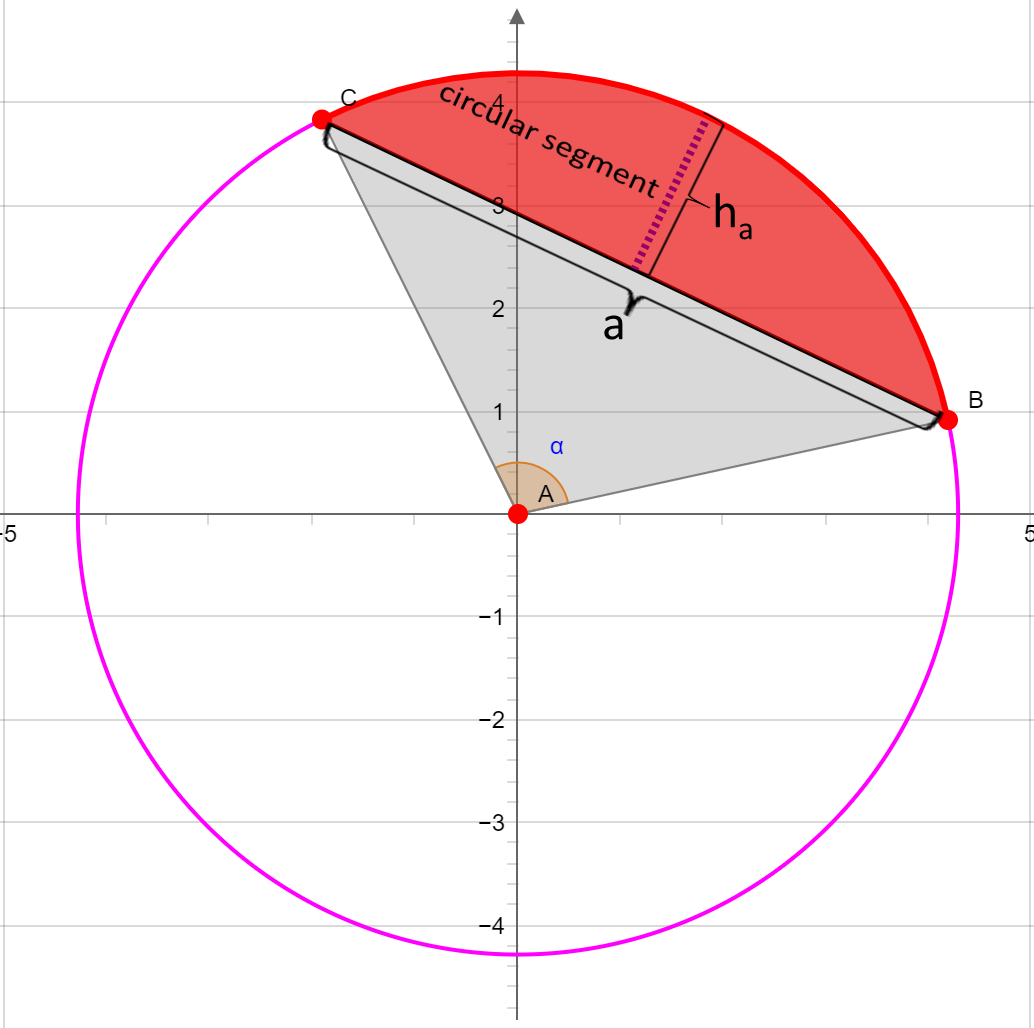
Area of the circular segment:

The circular segment is the area between the secant and the circle circumference. The area S_a of the circular segment is:

$S_{a} = \frac{r^{2}}{2} (α - \sin α)$

Height of the circular segment:

The height h_a of the circular segment is:

$h_{a} = r - \sqrt{r^{2} - \frac{a^{2}}{4}}$

Circle ring

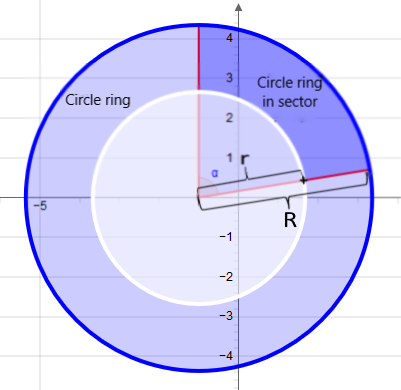
Area of the circle ring:

The circular ring is the area between the inner circle and the outer circle. Both circles have the same centre and differ in the radii R and r. The surface F_R of the circular ring is:

$F_{R} = π (R^{2} - r^{2})$

Area of the circle ring in sector:

The circular ring area which is limited from a circular ring by a sector with the opening angle α in radians:

$S_{R} = \frac{α π}{2} (R^{2} - r^{2})$

Screenshot of the circle image

Print or save the circle image via right mouse click.

Releated sites

Here is a list of of further useful sites:

Index Trigonometric calculations Ellipse Triangle Parallelogram Rectangle