Complex Numbers Calculus

Definitions and notations for complex numbers

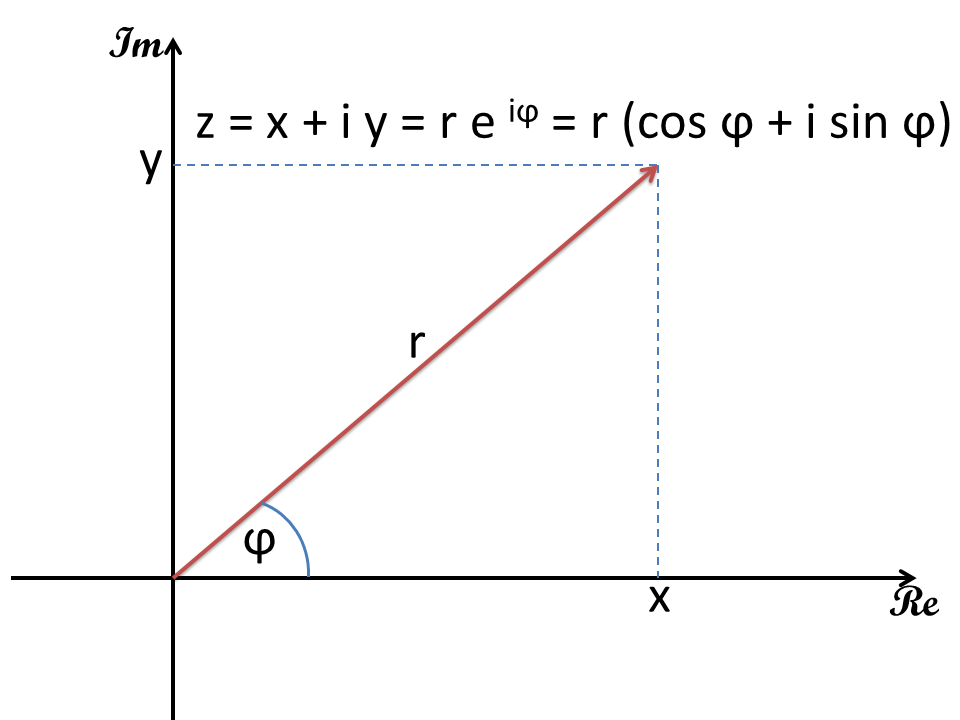
The complex numbers are an extension of the real numbers. Many computational rules of real numbers can be applied to complex numbers.

The theory of analytic functions dealt with functions of a complex variable.

The Origin of complex numbers is due to the release of algebraic equations. The origin of the theory of imaginary numbers, that is, all numbers whose square is a negative real number, going to the Italian mathematician Gerolamo Cardano and Rafael Bombelli in the 16th Century. The introduction of the imaginary unit i as the new number is attributed to Leonhard Euler.

The complex numbers are two-dimensional and can be used as vectors in the Gaussian plane of numbers represent. On the horizontal axis (Re) of the real part and on the vertical axis is applied (Im) of the imaginary part of the complex number. Vectors may also be similar to either the complex number in Cartesian coordinates (x, y) or polar coordinates (r, φ) can be expressed.

A complex number z consists of a real part x and an imaginary part y. The imaginary part is characterized by the imaginary unit i.

$z = x + i y$

$with x, y \in R and i = \sqrt{-1}$

The complex conjugate to z consists of a real part x and the negative imaginary part y. This corresponds to a reflection in the real axis in the Gaussian plane.

$\overline{z} = x - i y$

The amount of a complex number corresponds in the Gaussian plane with the length of the vector.

$| z | = \sqrt{x^{2} + y^{2}}$

The complex number in polar coordinates:

$z = r (\cos φ + i \sin φ) = r e^{i φ}$

with

$r = | z | = \sqrt{x^{2} + y^{2}}$

and

$φ = atan \frac{y}{x}$

and the Euler Formula

$\cos φ + i \sin φ = e^{i φ}$

Complex numbers graphical

Relationships of complex conjugate numbers

For complex conjugate numbers, the following relations hold.

$\overline{z} = z if z real is;$

$\overline{z_{1} + z_{2}} = \overline{z_{1}} + \overline{z_{2}}$

$\overline{z_{1} \cdot z_{2}} = \overline{z_{1}} \cdot \overline{z_{2}}$

$\overline{(\frac{z_{1}}{z_{2}})} = \frac{\overline{z_{1}}}{z_{2}}$

$z \cdot \overline{z} = x^{2} + y^{2}$

Rules for computing with complex numbers

Addition and subtraction of complex numbers

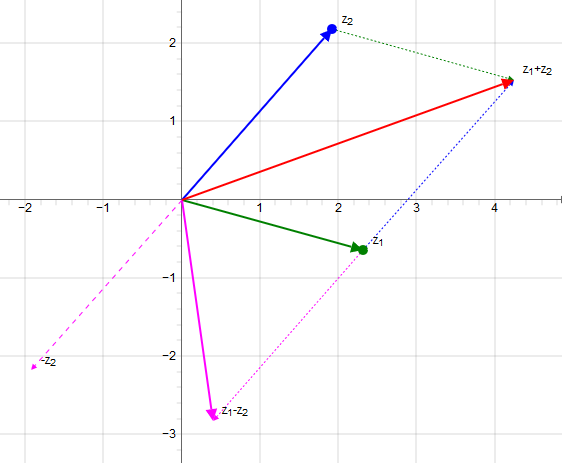
The addition and subtraction of complex numbers corresponding to the addition and subtraction of the position vectors. That the real and imaginary components are added or subtracted.

$With z_{1} = x_{1} + i y_{1} and z_{2} = x_{2} + i y_{2} is$

$z_{1} + z_{2} = x_{1} + x_{2} + i (y_{1} + y_{2})$

$z_{1} - z_{2} = x_{1} - x_{2} + i (y_{1} - y_{2})$

Graphical addition of complex numbers

Multiplication of complex numbers

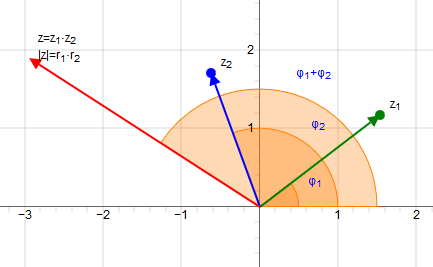
The multiplication is done by multiplying out the brackets considering the relation i²= -1.

$With z_{1} = x_{1} + i y_{1} and z_{2} = x_{2} + i y_{2} is$

$z_{1} \cdot z_{2} = (x_{1} + i y_{1}) \cdot (x_{2} + i y_{2})$ $= x_{1} \cdot x_{2} - y_{1} \cdot y_{2} + i (x_{1} \cdot y_{2} + y_{1} \cdot x_{2})$

The multiplication of complex numbers can also be done in trigonometric or exponential form.

$With z_{1} = r_{1} (\cos φ + i \sin φ) = r_{1} e^{i φ}$

$and z_{2} = r_{2} (\cos ψ + i \sin ψ) = r_{2} e^{i ψ} is$

$z_{1} \cdot z_{2}$ $= r_{1} r_{2} (\cos (φ + ψ) + i \sin (φ + ψ))$ $= r_{1} r_{2} e^{i (φ + ψ)}$

Graphical multiplication of complex numbers

Calculator: Multiplication of complex numbers

Division of complex numbers

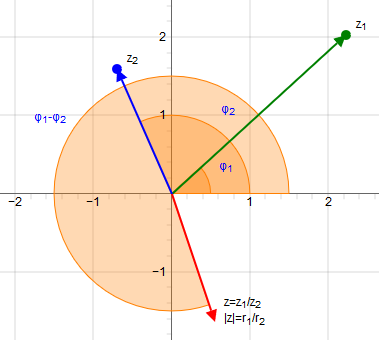
The division is carried out by the fraction is expanded with the complex conjugate of the denominator.

$With z_{1} = x_{1} + i y_{1} and z_{2} = x_{2} + i y_{2} is$

$\frac{z_{1}}{z_{2}} = \frac{x_{1} + i y_{1}}{x_{2} + i y_{2}}$ $= \frac{x_{1} + i y_{1}}{x_{2} + i y_{2}} \frac{x_{2} - i y_{2}}{x_{2} - i y_{2}}$ $= \frac{x_{1} x_{2} + y_{1} y_{2}}{x_{2}^{2} + y_{2}^{2}} + i \frac{x_{2} y_{1} - x_{1} y_{2}}{x_{2}^{2} + y_{2}^{2}}$

The division of complex numbers can also be done in trigonometric or exponential form.

$With z_{1} = r_{1} (\cos φ + i \sin φ) = r_{1} e^{i φ}$

$and z_{2} = r_{2} (\cos ψ + i \sin ψ) = r_{2} e^{i ψ} is$

$\frac{z_{1}}{z_{2}}$ $= \frac{r_{1}}{r_{2}} (\cos (φ - ψ) + i \sin (φ - ψ))$ $= \frac{r_{1}}{r_{2}} e^{i (φ - ψ)}$

Graphical division of complex numbers

Calculator: Division of complex numbers

Basic complex functions f(z)

Complex number cartesian

$z = x + i y$

Real part

$Re(z) = x$

Imaginary part

$Im(z) = y$

Conjugate

$\overline{z} = x - i y$

Amount

$| z | = \sqrt{x^{2} + y^{2}}$

Argument

$arg(z) = φ = atan \frac{y}{x}$

Polar

$z = | z | (\cos φ + i \sin φ)$

Square

$z^{2} = x^{2} - y^{2} + i x y$

Reciprocal

$\frac{1}{z} = \frac{x}{x^{2} + y^{2}} + i \frac{-y}{x^{2} + y^{2}}$

Square reciprocal

$\frac{1}{z^{2}} = \frac{x^{2} - y^{2}}{{(x^{2} + y^{2})}^{2}} + i \frac{- 2 x y}{{(x^{2} + y^{2})}^{2}}$

Square root

$\sqrt{z} = \pm \sqrt{\frac{x + \sqrt{x^{2} + y^{2}}}{2}} \pm i \sqrt{\frac{- x + \sqrt{x^{2} + y^{2}}}{2}}$

Exponential function

$e^{z} = e^{x} \cos y + i e^{x} \sin y$

Logarithm

$\ln z = \frac{1}{2} \ln (x^{2} + y^{2}) + i atan \frac{y}{x}$

Sine

$\sin z = \sin x \cosh y + i \cos x \sinh y$

Cosine

$\cos z = \cos x \cosh y - i \sin x \sinh y$

Sine hyperbolicus

$\sinh z = \sinh x \cos y + i \cosh x \sin y$

Cosine hyperbolicus

$\cosh z = \cosh x \cos y - i \sinh x \sin y$

Tangent

$\tan z = \frac{\sin 2 x}{\cos 2 x + \cosh 2 y} + i \frac{\sinh 2 y}{\cos 2 x + \cosh 2 y}$

Calculator for the function values

Powers of complex numbers

The power of a complex number in the n-th potency is done by using the formula of Moivre.

$z^{n}$ $= r^{n} (\cos n φ + i \sin n φ)$ $= r^{n} e^{i n φ}$

$with r = | z | = \sqrt{x^{2} + y^{2}}$

$and φ = atan \frac{y}{x}$

$and i^{0} = 1, i^{1} = i, i^{2} = - 1, i^{3} = - i ...$

$and n \in N$

or with the binomial theorem

$z^{n} = {(x + i y)}^{n} = \sum_{k = 0, k even}^{n} (\begin{matrix} n \\ k \end{matrix}) {(- 1)}^{\frac{k}{2}} x^{n - k} y^{k} + i \sum_{k = 1, k odd}^{n} (\begin{matrix} n \\ k \end{matrix}) {(- 1)}^{\frac{k - 1}{2}} x^{n - k} y^{k}$

Calculator: Complex Binomial Theorem

The calculator computes the power of the given complex number with the binomial theorem.

For general complex exponents is:

$z^{ω} = e^{ω \ln z}$

with z^ω as main value. If ω is not rational so there are infinite number of solutions.

Graphical power complex numbers

Calculator (Cartesian)

The calculator converts the given complex number from cartesian representation to the polar form. The angle is in radian.

Complex number cartesian

Conjugate complex number

Amount

Angle

Polar

Calculator (Polar)

The calculator converts the given complex number from polar representation to the cartesian form. The angle is in radian.

Complex number polar

Complex number cartesian

Conjugate

Amount

Complex Numbers Calculus

Definitions and notations for complex numbers

Relationships of complex conjugate numbers

Rules for computing with complex numbers

Addition and subtraction of complex numbers

Multiplication of complex numbers

Calculator: Multiplication of complex numbers

Division of complex numbers

Calculator: Division of complex numbers

Basic complex functions f(z)

Powers of complex numbers

Calculator: Complex Binomial Theorem

Calculator (Cartesian)

Calculator (Polar)

Releated sites