Calculatrice en ligne de trigonométrie

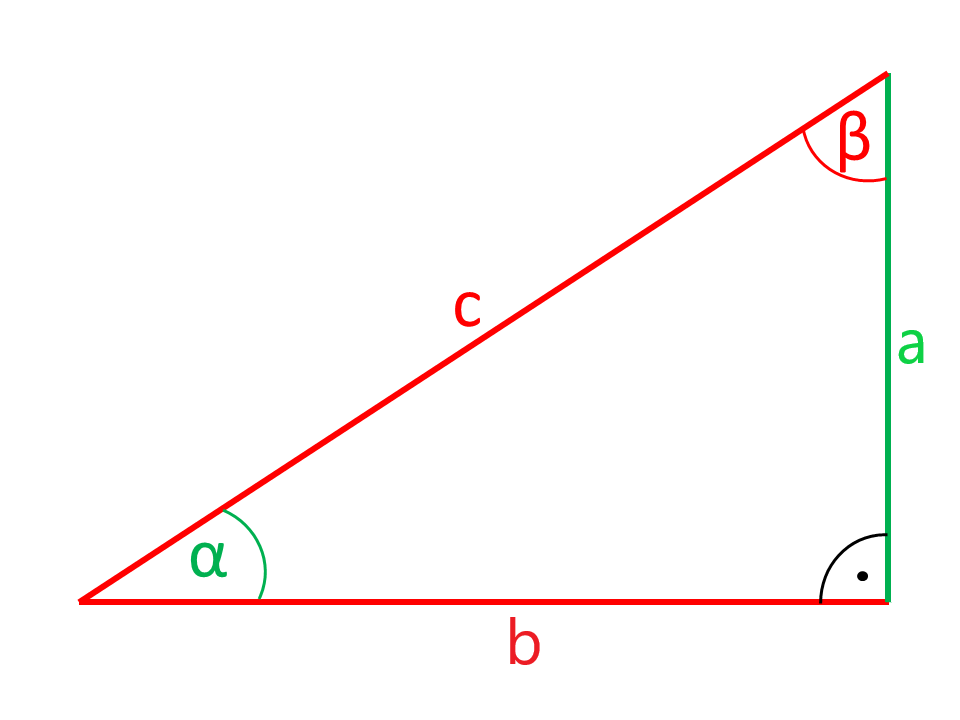
Calculatrice pour le triangle rectangle

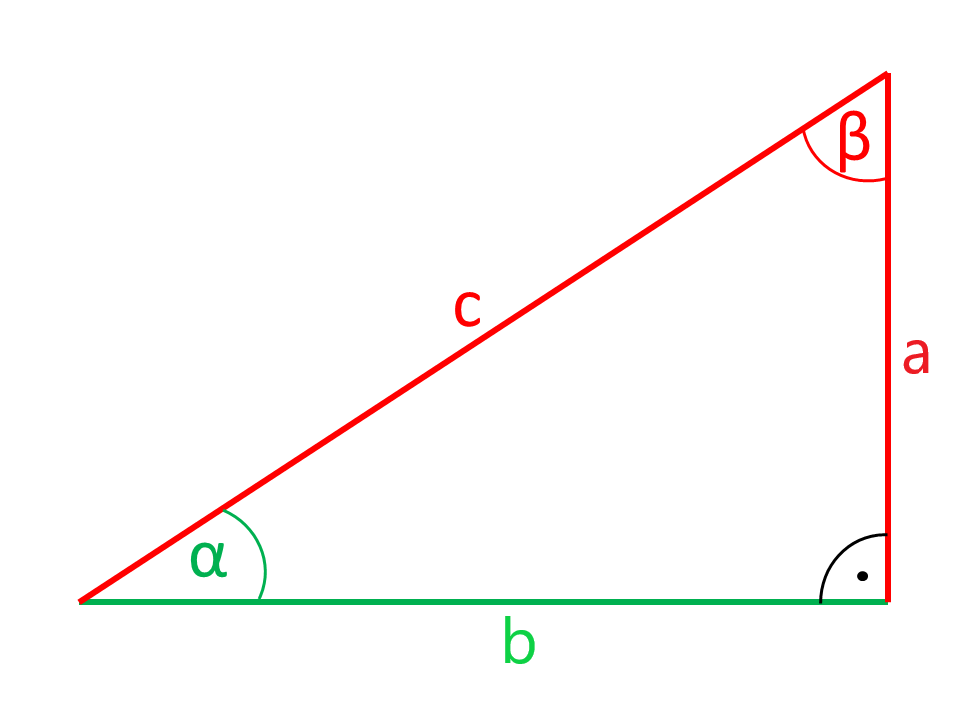
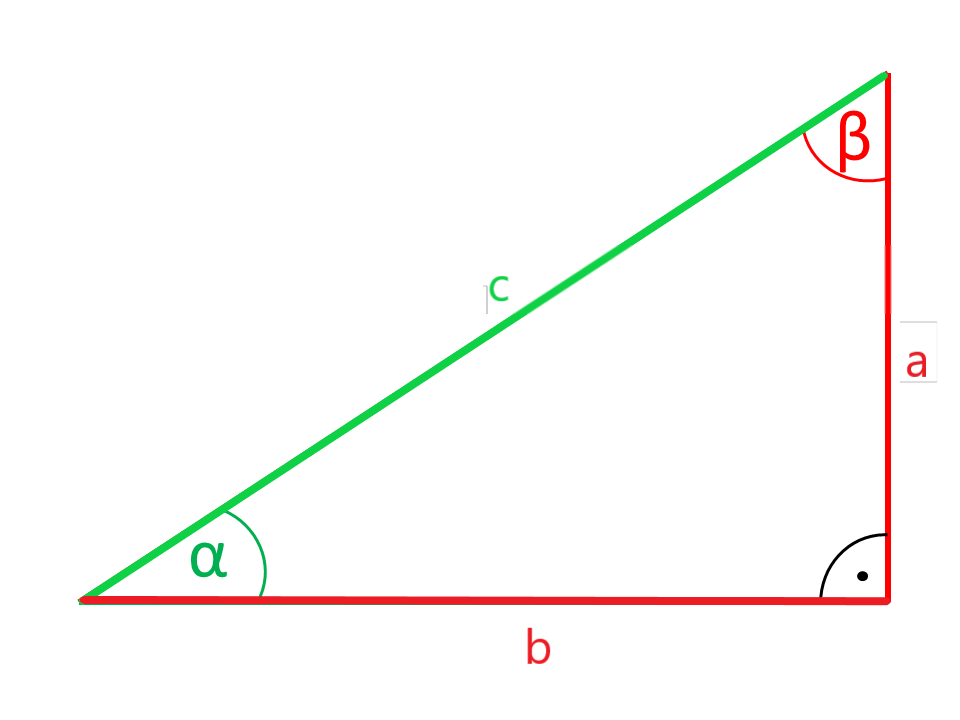
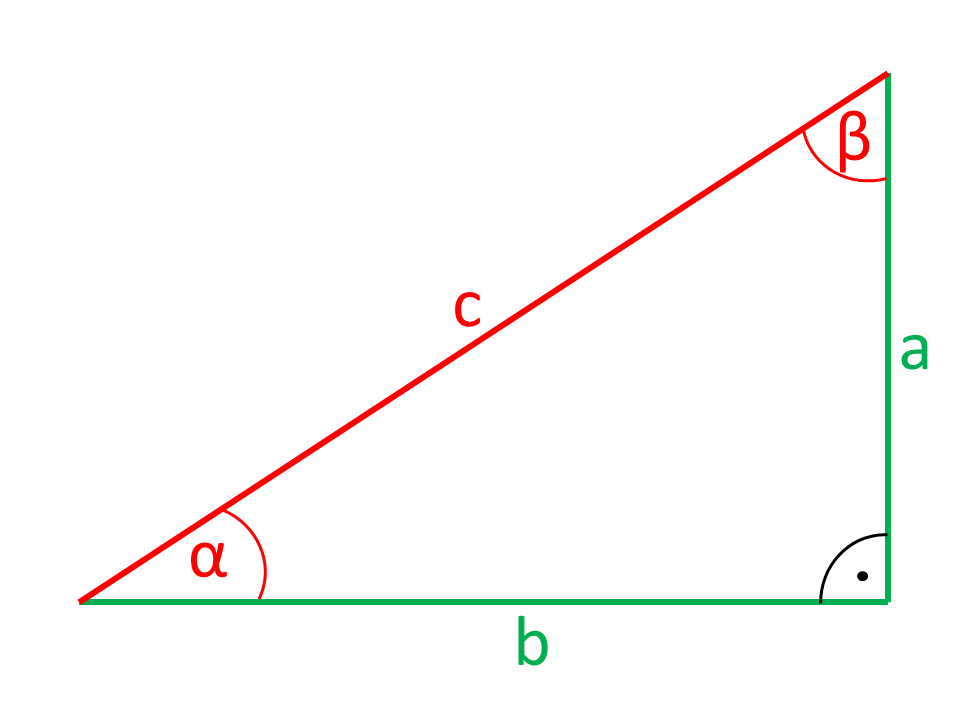
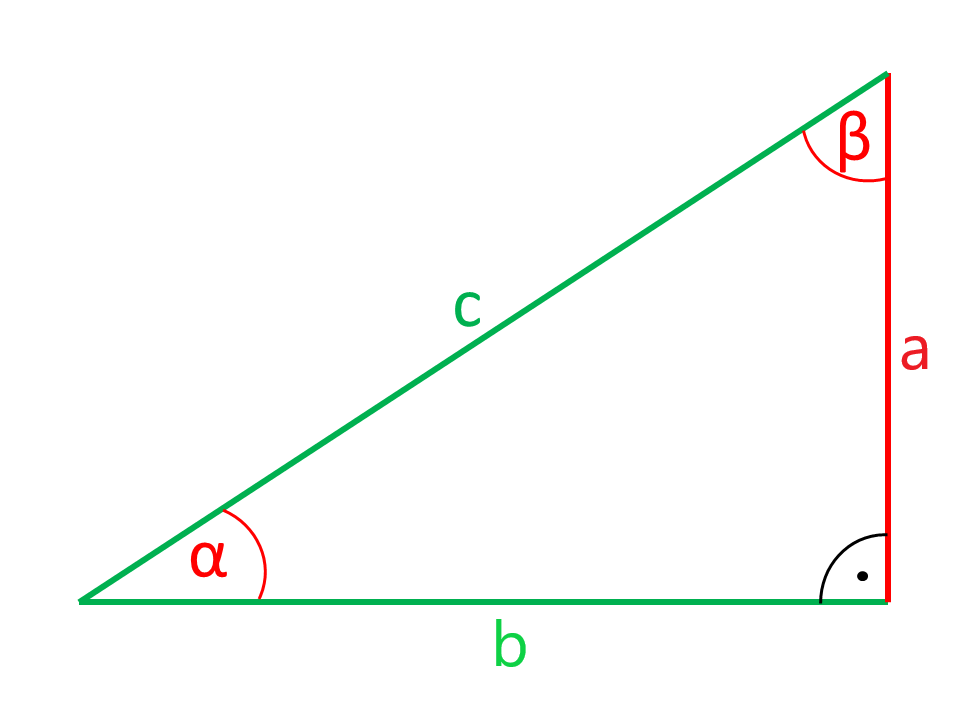
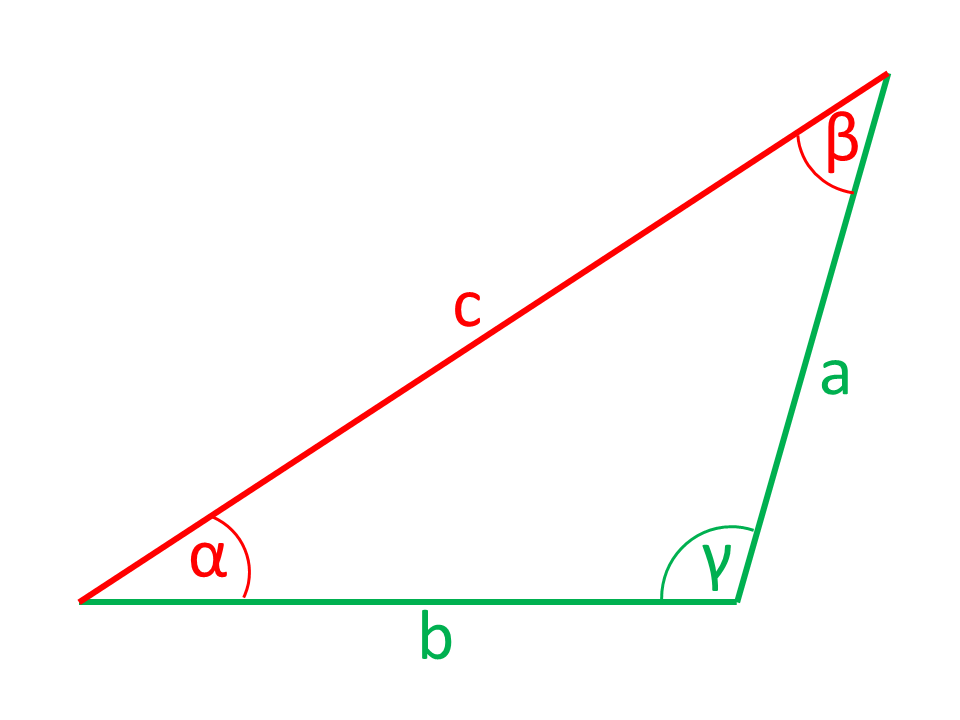
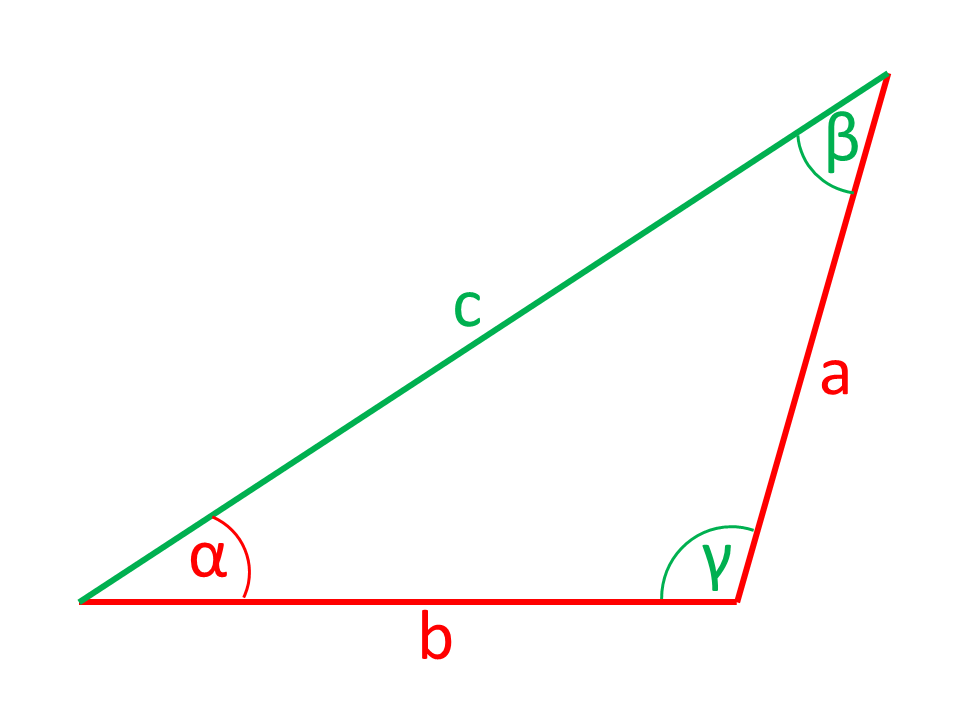
Les côtés ou les angles sont indiqués dans les illustrations en couleur rouge sont calculés par la calculatrice à partir des côtés et des angles indiqués en couleur verte.

.

Angle et cathetus opposé

α en degré =

a =

Angle et cathetus adjacent

α en degré =

b =

Angle et hypoténuse

α en degré =

c =

Cathetus

a =

b =

Cathetus et hypoténuse

b =

c =

Calculatrice pour les triangles généraux

Deux côtés et un angle

γ en degré =

a =

b =

Deux angles et un côté

γ en degré =

β en degré =

c =

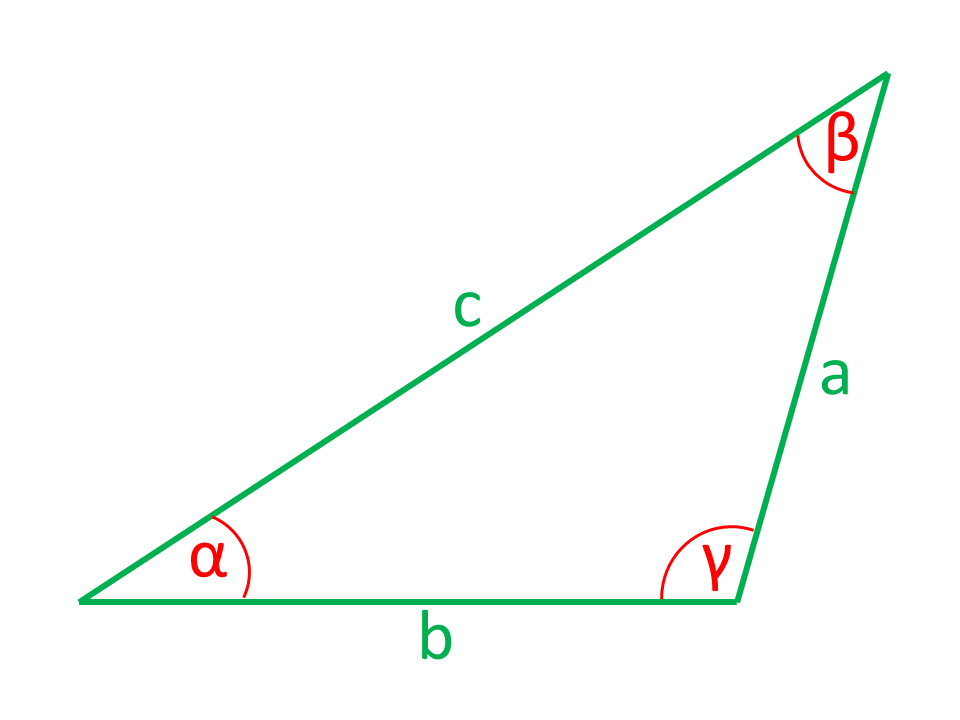
Trois côtés

a =

b =

c =

Exemples de calculs trigonométriques

Voici quelques exemples qui illustrent l'application des formules trigonométriques.

Exemple : Calcul de la hauteur d'une tour

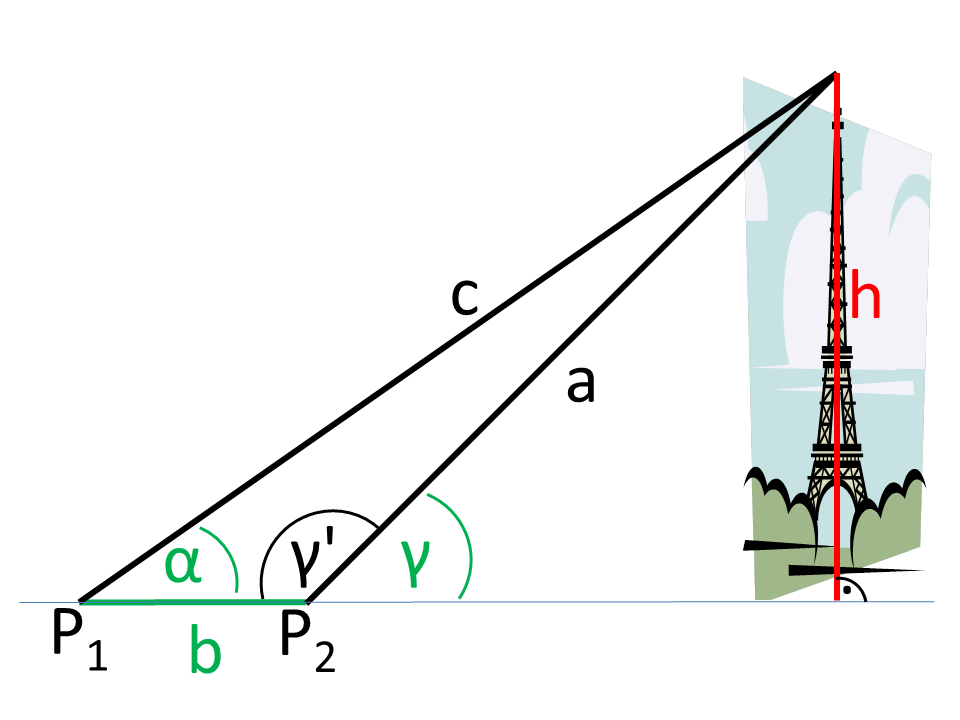
L'exemple montre comment une hauteur peut être déterminée, même si un accès direct n'est pas possible.

La figure montre que les angles de vue (α, γ) et la distance b des positions ont été déterminés à partir de deux positions (P₁, P₂) (en vert sur l'Illustration).

Un triangle est formé à partir de P₁, P₂, et de la pointe de la tour. De ce triangle général, on connaît l'angle &alpha ; et le côté b. L'angle &gamma ; peut être calculé comme suit:

$\mathrm{\gamma \text{'}}=180-\mathrm{\gamma }$

L'angle encore manquant &beta ; peut être déterminé, puisque la somme angulaire dans le triangle est de 180°.

.

$\beta =180-\mathrm{\alpha }-\mathrm{\gamma \text{'}}=\mathrm{\gamma }-\mathrm{\alpha }$

Dans l'étape suivante, on utilise l'ensemble des sinus pour calculer le côté a. Le côté a est un côté commun du triangle général et du triangle rectangle formé par a et la hauteur de la tour et la ligne de base.

.

$a=\sin \left(\alpha \right)\frac{b}{\sin \left(\beta \right)}=b\frac{\sin \left(\alpha \right)}{\sin \left(\gamma -\alpha \right)}$

Dans le triangle rectangle, a est l'hypoténuse, et h est la branche opposée de l'angle &gamma ;. La hauteur souhaitée h peut donc être calculée à l'aide de la fonction angulaire.

>

$h=a\sin \left(\gamma \right)=b\frac{\sin \left(\alpha \right)\sin \left(\gamma \right)}{\sin \left(\gamma -\alpha \right)}$

Alternativement, la hauteur de la tour peut également être calculée en appliquant deux équations pour le triangle rectangle. Le premier triangle est constitué de P₁ et de la base de la tour ainsi que de la pointe de la tour. Le second analogue sortant de P₂.

.

C'est :

$\tan \gamma =\frac{h}{x}$

et

$\tan \alpha =\frac{h}{b+x}$

avec la distance inconnue x de P₂ au point de base de la tour.

La reformulation des équations aboutit dans chaque cas à :

$x=\frac{h}{\tan \gamma }$

et

$x=\frac{h-b\tan \alpha }{\tan \alpha }$

En mettant les équations à égalité et en résolvant pour h, on obtient la solution:

$h=b\frac{\tan \alpha \tan \gamma }{\tan \gamma -\tan \alpha }$

Les deux solutions pour h sont équivalentes peut être facilement prouvé en remplaçant de

$\tan \left(\alpha \right)=\frac{\sin \left(\alpha \right)}{\cos \left(\alpha \right)}$

et

$\tan \left(\gamma \right)=\frac{\sin \left(\gamma \right)}{\cos \left(\gamma \right)}$

$h=b\frac{\tan \alpha \tan \gamma }{\tan \gamma -\tan \alpha }=b\frac{\sin \alpha \sin \gamma }{\sin \gamma \cos \alpha -\sin \alpha \cos \gamma }$

Avec le théorème de l'addition

$\sin \left(x\pm y\right)=\sin \left(x\right)\cos \left(y\right)\pm \cos \left(x\right)\sin \left(y\right)$

les résultats de la solution ci-dessus.

Il est

$h=b\frac{\tan \alpha \tan \gamma }{\tan \gamma -\tan \alpha }=b\frac{\sin \left(\alpha \right)\sin \left(\gamma \right)}{\sin \left(\gamma -\alpha \right)}$

Exemple : Palier transversal

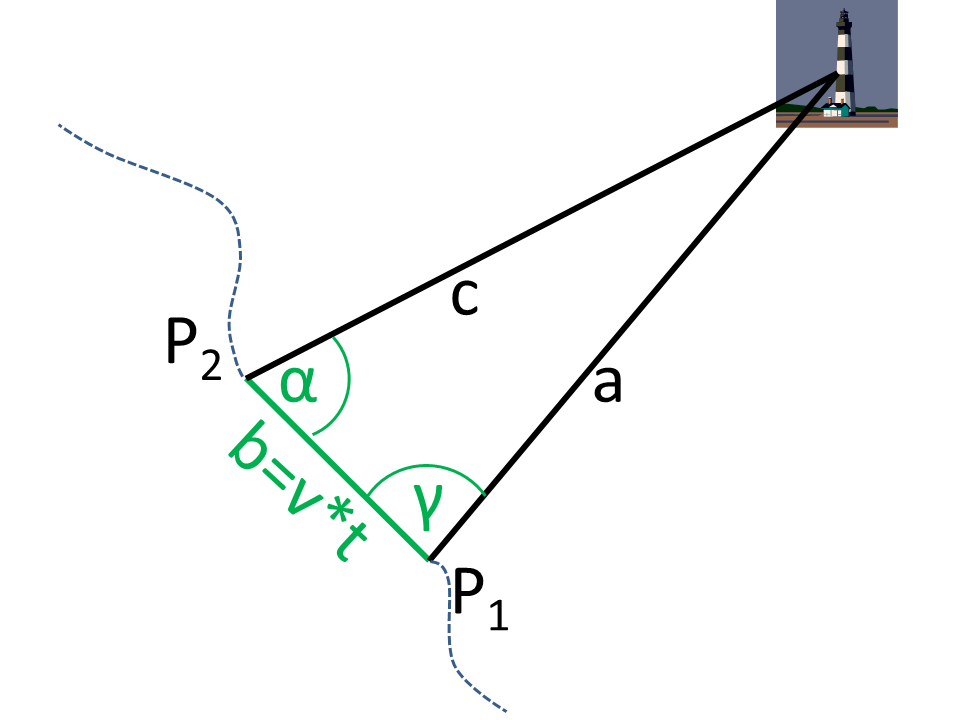
Un point fixe (par exemple, un phare) depuis deux positions est visé par le relèvement transversal. Un cap constant et une vitesse constante sont appliqués entre les deux relèvements (P₁, P₂). Ensuite, la distance du point cible peut être déterminée à partir des roulements.

La figure montre que les angles de vue (α, γ) par rapport à la direction du déplacement ont été déterminés à deux positions (P₁, P₂) (en vert sur la figure). La longueur du côté b est obtenue à partir de la vitesse v et de l'intervalle de temps t des mesures.

Un triangle est formé à partir de P₁, P₂ et du point cible (phare). De ce triangle général, on connaît l'angle &alpha ; et le côté b = v * t.

.

L'angle &beta ; encore manquant peut être déterminé, puisque la somme angulaire dans le triangle est de 180°.

$\beta =180-\mathrm{\alpha }-\mathrm{\gamma }$

Dans l'étape suivante, la règle des sinus est utilisée pour calculer le côté a. Le côté a est la distance du point de mesure P₁.

$a=\sin \left(\alpha \right)\frac{b}{\sin \left(\beta \right)}$

La distance au second point de mesure est calculée de manière analogue.

$c=\sin \left(\gamma \right)\frac{a}{\sin \left(\alpha \right)}$

Exemple : Mesure d'un itinéraire inaccessible (tâche de Hansen)

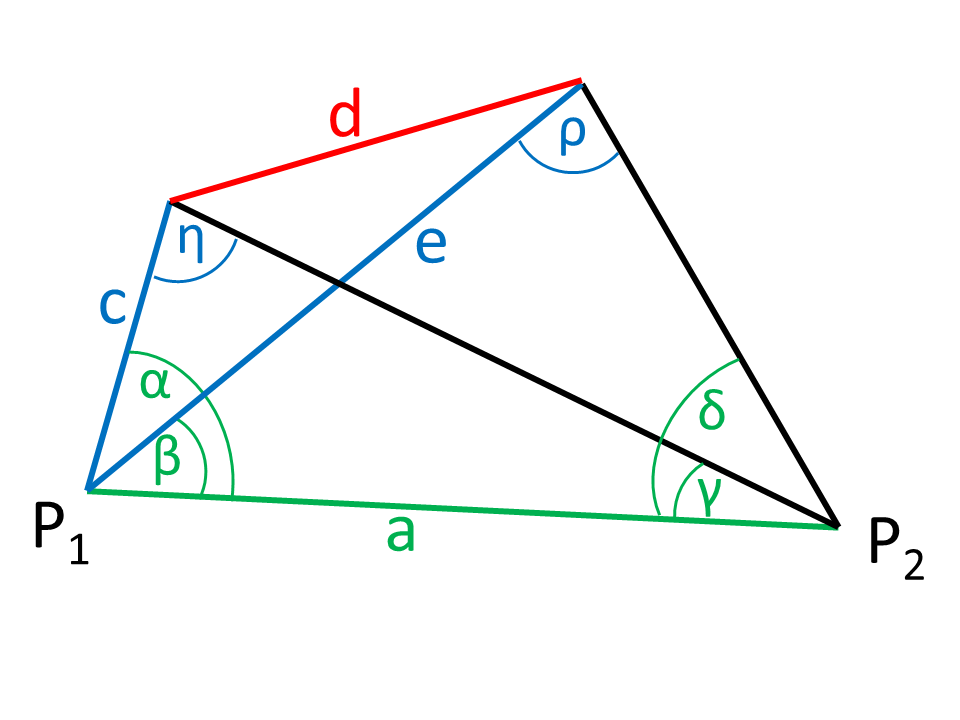
Pour mesurer un itinéraire inaccessible, on détermine le début et la fin de l'itinéraire à partir de deux points (P₁, P₂).

La figure montre que les angles de vue (α, β, γ, δ) à deux positions (P₁, P₂) par rapport à l'axe de liaison des points (en vert sur la figure). La distance a des points de mesure est également connue. Il s'agit de déterminer la longueur de la distance inaccessible d (rouge sur la figure).

La figure montre les valeurs bleues à calculer.

L'angle &eta ; peut être déterminé, puisque la somme angulaire dans le triangle est de 180°.

$\eta =180-\mathrm{\alpha }-\mathrm{\gamma }$

Dans l'étape suivante, la règle des sinus est utilisée pour calculer le côté c.

$c=a\frac{\sin \left(\gamma \right)}{\sin \left(\eta \right)}$

Le côté e est également calculé avec la règle du sinus.

$e=a\frac{\sin \left(\delta \right)}{\sin \left(\rho \right)}$

L'angle ρ résulte de la somme des angles dans un triangle.

$\rho =180-\mathrm{\beta }-\mathrm{\delta }$

La règle du cosinus peut maintenant être utilisée pour calculer la distance requise d.

$d^2=a^2+c^2-2ac\cos \left(\alpha -\beta \right)$

Exemple : Triangle des forces sur le pendule

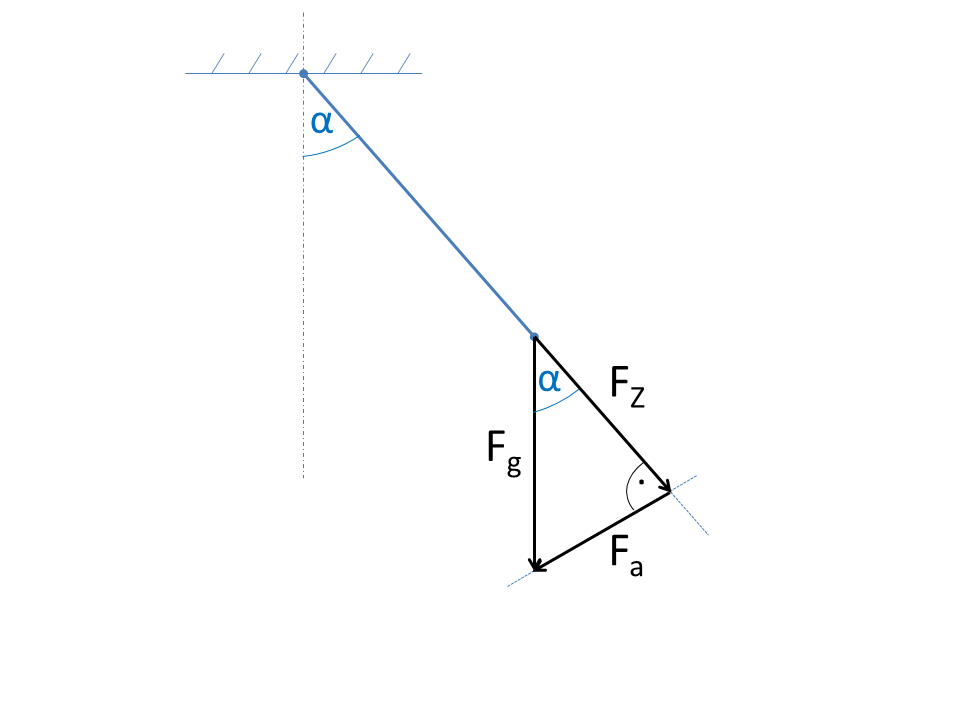
La décomposition des forces en composantes orthogonales joue un rôle important en mécanique. Cet exemple montre comment la force du poids peut être décomposée en deux composantes au moyen des fonctions d'angle.

La figure montre un pendule à fil avec une masse à l'extrémité du fil. La force de poids F _g doit être décomposée en forces partielles. La force dans la direction du fil F _Z ne contribue pas à l'accélération et la force F _a est donc pertinente pour l'équation du mouvement. Les forces partielles peuvent être décomposées en plusieurs forces.

Les forces partielles peuvent être spécifiées directement au moyen des fonctions d'angle, puisqu'elles constituent un triangle rectangle.

$F_a=F_g\sin \left(\alpha \right)$

$F_Z=F_g\cos \left(\alpha \right)$

Trigonométrie générale

La tâche de base de la Trigonométrie est (etc. Longueurs des côtés, tailles des angles, longueurs des triangles-transversaux) de calculer à partir de trois tailles d'un triangle donné d'autres tailles de ce triangle. Comme aide aux fonctions trigonométriques sinus (sin), cosinus (cos), tangente (tan), cotangente (cot). Précurseur de la trigonométrie il y avait déjà pendant l'Antiquité dans les mathématiques grecques. Aristarque de Samos a profité des propriétés des triangles droits pour calculer les rapports de distance entre la terre et le soleil et la lune.

Triangle à angle droit

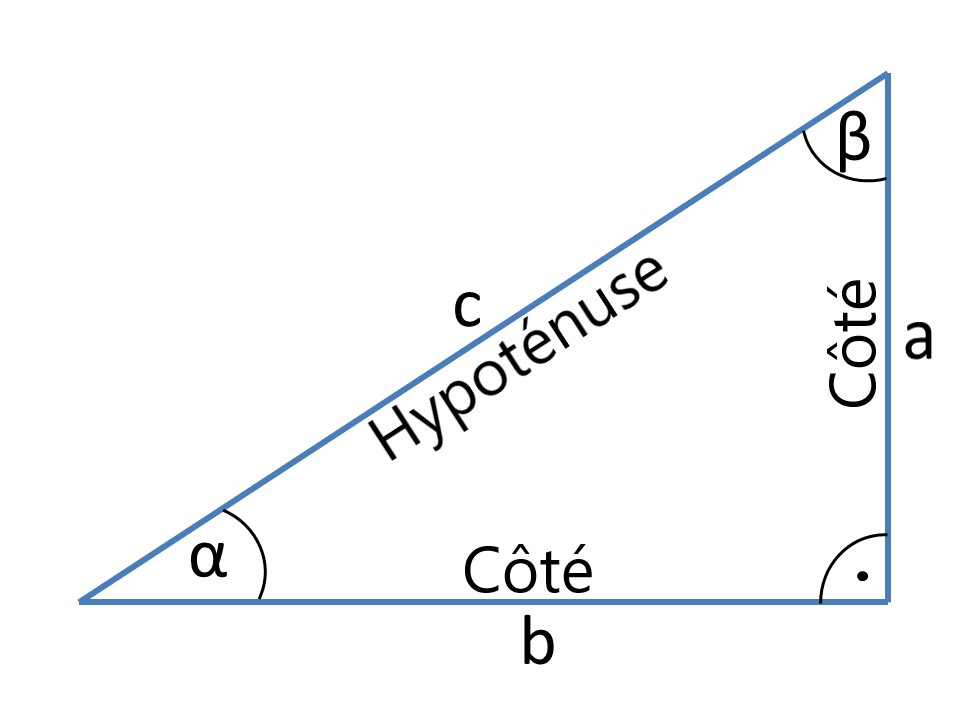
Définitions

Les côtés a et b du triangle rectangle, qui incluent l'angle droit sont les cathéters. L'angle droit opposé au côté c est l'hypoténuse. En regardant l'angle α comme le côté a est le côté adjacent et le côté opposé b.

Fonctions trigonométriques

$\sin \left(\alpha \right)=\cos \left(\beta \right)=\frac{a}{c}$

$\cos \left(\alpha \right)=\sin \left(\beta \right)=\frac{b}{c}$

$\tan \left(\alpha \right)=\cot \left(\beta \right)=\frac{a}{b}$

Degree / Radians

L'angle peut être spécifié en grado (deg) ou en radians (rad). Le cercle complet en degré est de 360 degré en radians il est de 2π. En conséquence, les conversions suivantes s'appliquent.

$\text{Angle (rad)}=\frac{\pi }{180}\text{Angle (deg)}$

$\text{Angle (deg)}=\frac{180}{\pi }\text{Angle (rad)}$

Somme des angles

La somme des angles d'un triangle est égale à 180°. On applique donc dans le triangle rectangle la relation suivante pour l'angle.

$90=\alpha +\beta$

Triangle général

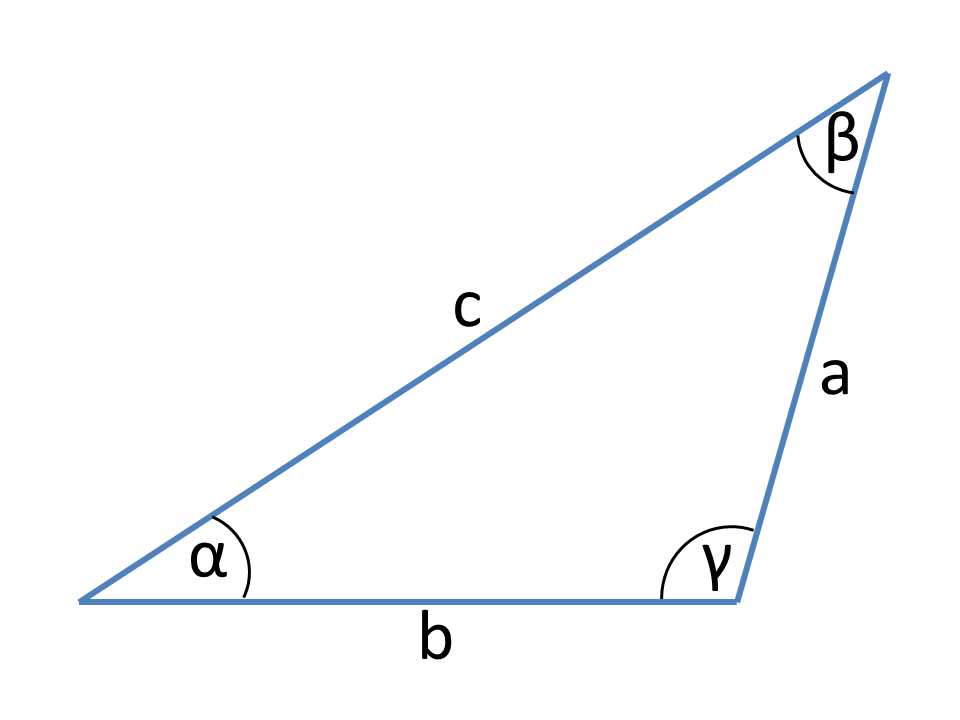
Définitions

Les essentiels pour les calculs en triangle général sont la loi du cosinus et du sinus et la relation des fonctions trigonométriques.

Loi sinusoïdale

$\frac{a}{\sin \left(\alpha \right)}=\frac{b}{\sin \left(\beta \right)}=\frac{c}{\sin \left(\gamma \right)}$

Loi du cosinus

$a^2=b^2+c^2-2bc\cos \left(\alpha \right)$

$b^2=a^2+c^2-2ac\cos \left(\beta \right)$

$c^2=a^2+b^2-2ab\cos \left(\gamma \right)$

Loi de projection

$c=a\cdot \cos \left(\beta \right)+b\cdot \cos \left(\alpha \right)$

Formule de la tangente

$\tan \left(\gamma \right)$$=\frac{c\cdot \sin \left(\alpha \right)}{b-c\cdot \cos \left(\alpha \right)}$$=\frac{c\cdot \sin \left(\beta \right)}{a-c\cdot \cos \left(\beta \right)}$

Somme des angles

La somme des angles d'un triangle beträt 180°.

$180=\alpha +\beta +\gamma$

Circonférence r

$r=\frac{s}{4\cdot \cos \left(\frac{\alpha }{2}\right)\cdot \cos \left(\frac{\beta }{2}\right)\cdot \cos \left(\frac{\gamma }{2}\right)}$

avec

$s=\frac{1}{2}\left(a+b+c\right)$

Rayon du cercle inscrit ρ

$\rho =\sqrt{\frac{\left(s-a\right)\left(s-b\right)\left(s-c\right)}{s}}$

Hauteur h_c sur c

$h_c=a\cdot \sin \left(\beta \right)=b\cdot \sin \left(\alpha \right)$

Aire A

$A=\frac{1}{2}a\cdot b\cdot \sin \left(\gamma \right)$

Formule d'aire heronische

$A=\rho s=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}$

Propriétés des fonctions trigonométriques

Formules réductrices (en degré)

$\sin \left(\mathrm{90°}+x\right)=\cos \left(x\right)$

$\cos \left(\mathrm{90°}+x\right)=-\sin \left(x\right)$

$\tan \left(\mathrm{90°}+x\right)=-\cot \left(x\right)$

$\cot \left(\mathrm{90°}+x\right)=-\tan \left(x\right)$

$\sin \left(\mathrm{180°}+x\right)=-\sin \left(x\right)$

$\cos \left(\mathrm{180°}+x\right)=-\cos \left(x\right)$

$\tan \left(\mathrm{180°}+x\right)=\tan \left(x\right)$

$\cot \left(\mathrm{180°}+x\right)=\cot \left(x\right)$

Fonctions trigonométriques à arguments égaux

${\sin \left(x\right)}^2+{\cos \left(x\right)}^2=1$

$\tan \left(x\right)=\frac{\sin \left(x\right)}{\cos \left(x\right)}$

Théorème d'addition des fonctions trigonométriques

$\sin \left(x\pm y\right)=\sin \left(x\right)\cos \left(y\right)\pm \cos \left(x\right)\sin \left(y\right)$

$\cos \left(x\pm y\right)=\cos \left(x\right)\cos \left(y\right)\mp \sin \left(x\right)\sin \left(y\right)$

$\tan \left(x\pm y\right)=\frac{\tan \left(x\right)\pm \tan \left(y\right)}{1\mp \tan \left(x\right)\tan \left(y\right)}$

Autres calculatrices

Voici une liste d'autres calculatrices utiles:

Contenu du site

Trigonométrie

Trigonométrie tabels Calculateur de puissances et d'arguments n-fois du sinus et du cosinus Calculateur d'triangle