Forma del vertice
Calcolatrice per la conversione dalla forma standard alla forma del vertice
La calcolatrice determina la forma del vertice della funzione quadratica passo dopo passo.
La funzione quadratica generale
viene convertito nella forma di vertice
Inserisci i coefficienti a, b e c della funzione quadratica:
Conversione alla forma del vertice con Espansione quadratica:
Il risultato è la forma del vertice:
La forma del vertice della funzione quadrata è:
o se la funzione quadrata è in forma base con a=1:
Dove xV e yV sono le coordinate x e y del vertice della parabola. Il vertice è il minimo o il massimo della funzione, a seconda che la parabola sia ascendente o discendente.
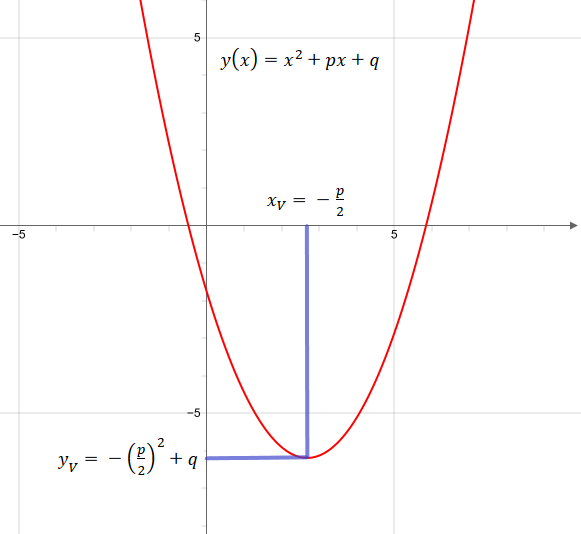
Vertice di una parabola in forma p,q
Vertice di una parabola in forma generale
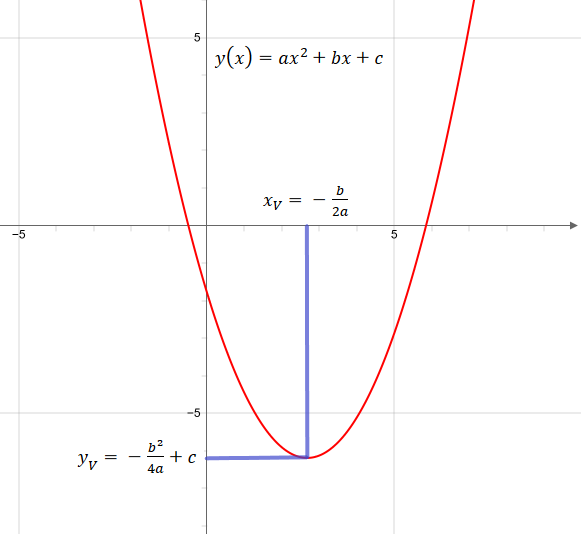
Vertice della parabola
La determinazione del vertice di una funzione quadratica si esegue derivando la funzione. La condizione per un estremo è che la derivata prima della funzione svanisca. Per una funzione quadratica questo è sufficiente per un minimo o un massimo.
Il punto di partenza è la funzione quadratica generale:
La derivata della forma generale è:
La condizione per il vertice è che la derivata sia 0. Ciò significa che la seguente equazione è valida:
Risolvendo si ottiene la coordinata x del vertice:
Inserendo nella funzione quadratica generale si ottiene la coordinata y del vertice:
Dalla derivata seconda della funzione quadratica segue se il vertice è un massimo o un minimo. La derivata seconda è:
Quindi per a > 0 il vertice è un valore minimo della parabola e per a < 0 un valore massimo.
Trasformazione dalla forma base alla forma del vertice
Nella forma base, il coefficiente prima di x2 è uguale a 1. La forma base della funzione quadratica con i coefficienti costanti p e q è
Se la funzione quadrata è in forma base, il vertice della parabola è dato da:
Trasformazione dalla forma base alla forma del vertice con espansione quadratica e applicazione del primo binomio:
Calcolatrice per la conversione dalla forma base alla forma del vertice
Inserisci i coefficienti p e q dell'equazione quadratica:
Conversione alla forma del vertice con espansione quadratica:
Trasformazione da forma standard a forma di vertice
Forma standard della funzione quadratica con i coefficienti costanti a, b e c:
Se la funzione quadratica è nella forma standard il vertice è dato da:
Trasformazione dalla forma standard alla forma del vertice con Espansione quadratica e Applicazione del primo binomio:
Dalla forma del vertice alla forma standard
Conversione della forma del vertice della funzione quadratica nella forma standard.
Il punto di partenza è la forma del vertice
Risolvendo il quadrato si ottiene:
Moltiplicando la parentesi si ottiene:
Inserimento di xV e yV risultati:
L'accorciamento si traduce in:
Le sommatorie si annullano a vicenda e la funzione quadratica generale segue:
Calcolo dei punti zero dalla forma del vertice
Dalla forma del vertice della funzione quadratica è facile calcolare gli zeri della funzione.
Partendo dalla forma del vertice
la condizione per gli zeri è che la funzione sia zero
e rimodellare i rendimenti
la radice quadrata porta a
e infine agli zeri
Altre calcolatrici
Qui c'è una lista di altre calcolatrici utili:
ContenutoDi più
Media mobile Calcolatrice della trasformata di Fourier Adattamento della curva Calcolatrice ellisse Calcolatrice cerchi Legge di azione di massa Risoluzione di equazioni quadratiche Forma normale a forma di vertice Equazione quadratica Metodo di Newton Calcolatrice di frazione