Vertex form

The vertex form of the square function is:

$y (x) = a {(x - x_{V})}^{2} + y_{V}$

or if the square funktion is in basic form with a=1:

$y (x) = {(x - x_{V})}^{2} + y_{V}$

Where x_V and y_V are the x and y coordinates of the vertex of the parabola. The vertex is the minimum or maximum of the function, depending on whether the parabola is up or down.

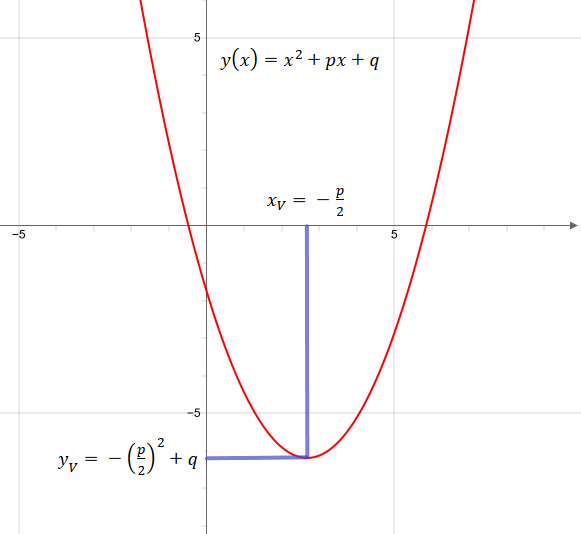
Vertex of a quadratic function in p,q-Form

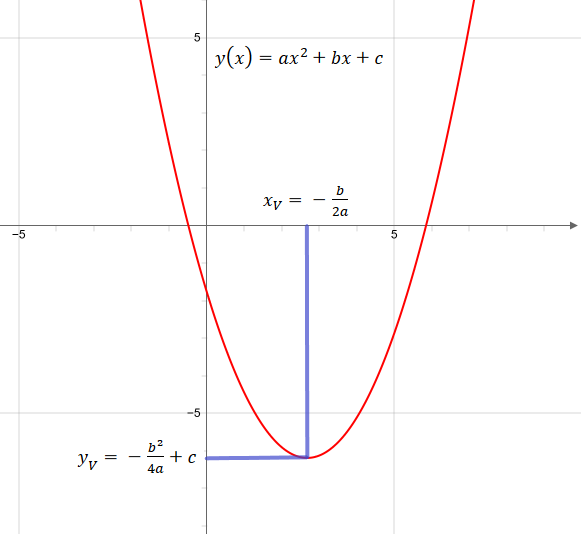
Vertex of a quadratic function in general form

Vertex of the parabola

The determination of the vertex of a quadratic function is performed by deriving the function. The condition for an extremum is that the first derivative of the function vanishes. For a square function this is sufficient for a minimum or maximum.

Start point is the general quadratic function:

$y (x) = a x^{2} + b x + c$

The derivative of the general form is:

$y' = 2 a x + b$

The condition for the vertex is that the derivative is 0. That means the following equation is valid:

$2 a x + b = 0$

Resolving yields the x coordinate of the vertex:

$x_{V} = - \frac{b}{2 a}$

Inserting into the general quadratic function yields the y-coordinate of the vertex:

$y_{V} = - \frac{b^{2}}{4 a} + c$

From the second derivative of the quadratic function follows wether the vertex is a maximum or minimum. The second derivative is:

$y'' = 2 a$

So for a > 0 the vertex is a minimum value of the parabola and for a < 0 a maximum value.

Transformation from basic form to vertex form

In the basic form, the coefficient before x² is equal to 1. The basic form of the quadratic function with the constant coefficients p and q is

$y (x) = x^{2} + p x + q$

If the square function is in basic form, the vertex of the parabola is given by:

$x_{V} = - \frac{p}{2}$

$y_{V} = - {(\frac{p}{2})}^{2} + q$

Transformation from the basic form to the vertex form with quadratic expansion and application of the first binomial:

$x^{2} + p x + q =$

$x^{2} + p x + {(\frac{p}{2})}^{2} - {(\frac{p}{2})}^{2} + q =$

${(x + \frac{p}{2})}^{2} - {(\frac{p}{2})}^{2} + q =$

${(x - \frac{- p}{2})}^{2} - {(\frac{p}{2})}^{2} + q =$

${(x - x_{V})}^{2} + y_{V}$

Calculator for the conversion from the basic form to the vertex form

Input the coefficients p and q of the quadratic equation:

Conversion to the vertex form with quadratic expansion:

Transformation from standard form to vertex form

Standard form of the quadratic function with the constant coefficients a, b, and c:

$y = a x^{2} + b x + c$

If the quadratic function is in the standard form the vertex is given by:

$x_{V} = - \frac{b}{2 a}$

$y_{V} = - \frac{b^{2}}{4 a} + c$

Transformation from the standard form to the vertex form with quadratic expansion and application of the first binomial:

$a x^{2} + b x + c =$

$a (x^{2} + \frac{b}{a} x) + c =$

$a (x^{2} + \frac{b}{a} x + {(\frac{b}{2 a})}^{2} - {(\frac{b}{2 a})}^{2}) + c =$

$a (x^{2} + \frac{b}{a} x + {(\frac{b}{2 a})}^{2}) - \frac{b^{2}}{4 a} + c =$

$a {(x + \frac{b}{2 a})}^{2} - \frac{b^{2}}{4 a} + c =$

$a {(x - \frac{- b}{2 a})}^{2} - \frac{b^{2}}{4 a} + c =$

$a {(x - x_{V})}^{2} + y_{V}$

Calculator for the conversion from the standard form to the vertex form

Input the coefficients a, b and c of the quadratic function:

Conversion to the vertex form with quadratic expansion:

From vertex form to standard form

Conversion of the vertex form of the quadratic function into the standard form.

Starting point is the vertex form

$y = a {(x - x_{V})}^{2} + y_{V} =$

Resolving the square results in:

$a (x^{2} - 2 x x_{V} + {x_{V}}^{2}) + y_{V} =$

Multiplying out the bracket results in:

$a x^{2} - 2 a x x_{V} + a {x_{V}}^{2} + y_{V} =$

Insertion of x_V and y_V results:

$a x^{2} + 2 a x \frac{b}{2 a} + a {(- \frac{b}{2 a})}^{2} - \frac{b^{2}}{4 a} + c =$

Shortening results in:

$a x^{2} + b x + \frac{b^{2}}{4 a} - \frac{b^{2}}{4 a} + c =$

The summands cancel each other out and the general quadratic function follows:

$a x^{2} + b x + c$

Calculation of the zero points from the vertex shape

From the vertex form of the quadratic function it is easy to calculate the zeros of the function.

Starting from the vertex form

$y = a {(x - x_{V})}^{2} + y_{V}$

the condition for zeros is that the function is zero

$0 = a {(x - x_{V})}^{2} + y_{V}$

and reshaping yields

${(x - x_{V})}^{2} = - \frac{y_{V}}{a}$

square root leads to

$x - x_{V} = \pm \sqrt{- \frac{y_{V}}{a}}$

and finally to the zeros

$x_{1,2} = x_{V} \pm \sqrt{- \frac{y_{V}}{a}}$

More Calculators

The online calculator calculates the solutions of quadratic equations with solution steps.

Quadratic equation calculation rules Quadratic Equation Solver Parabola Plotter