Online Triangle Calculator

Interactive Triangle calculator

The triangle calculator calculates the angles, heights, area, incircle radius, Circumcircle radius, ...

Move the points in the grafic or define the point coordinates in the numeric field to define the triangle. The calulated results are shown in the table. The calculation formulas are given below.

⃢

↹#.000

🔍↔

🔍↕

Side length:

Heigths:

h_a=

h_b=

h_c=

Angles in degree:

α=

β=

γ=

Angles in radian:

α=

β=

γ=

Median lines:

m_a=

m_b=

m_c=

Bisector lines:

l_α=

l_β=

l_γ=

Circumference U=

Area =

Circle radii

Axes ranges

x-min=

x-max=

y-min=

y-max=

Definition of the triangle:

Point 1 coordinates x, y

P1 =

Point 2 coordinates x, y

P2 =

Point 3 coordinates x, y

P3 =

Side length

Angle

α=

β=

γ=

Styles for the fgrafic and selection of the displayed elements:

P₁, P₂, P₃:

Sides:

Incircle:

Circumcircle:

Heights:

Median lines:

Perpendicular lines:

Bisector lines:

Triangle calculation formulas

Angular sum

The angle sum in triangle is 180°.

$α + β + γ = 180 °$

Median

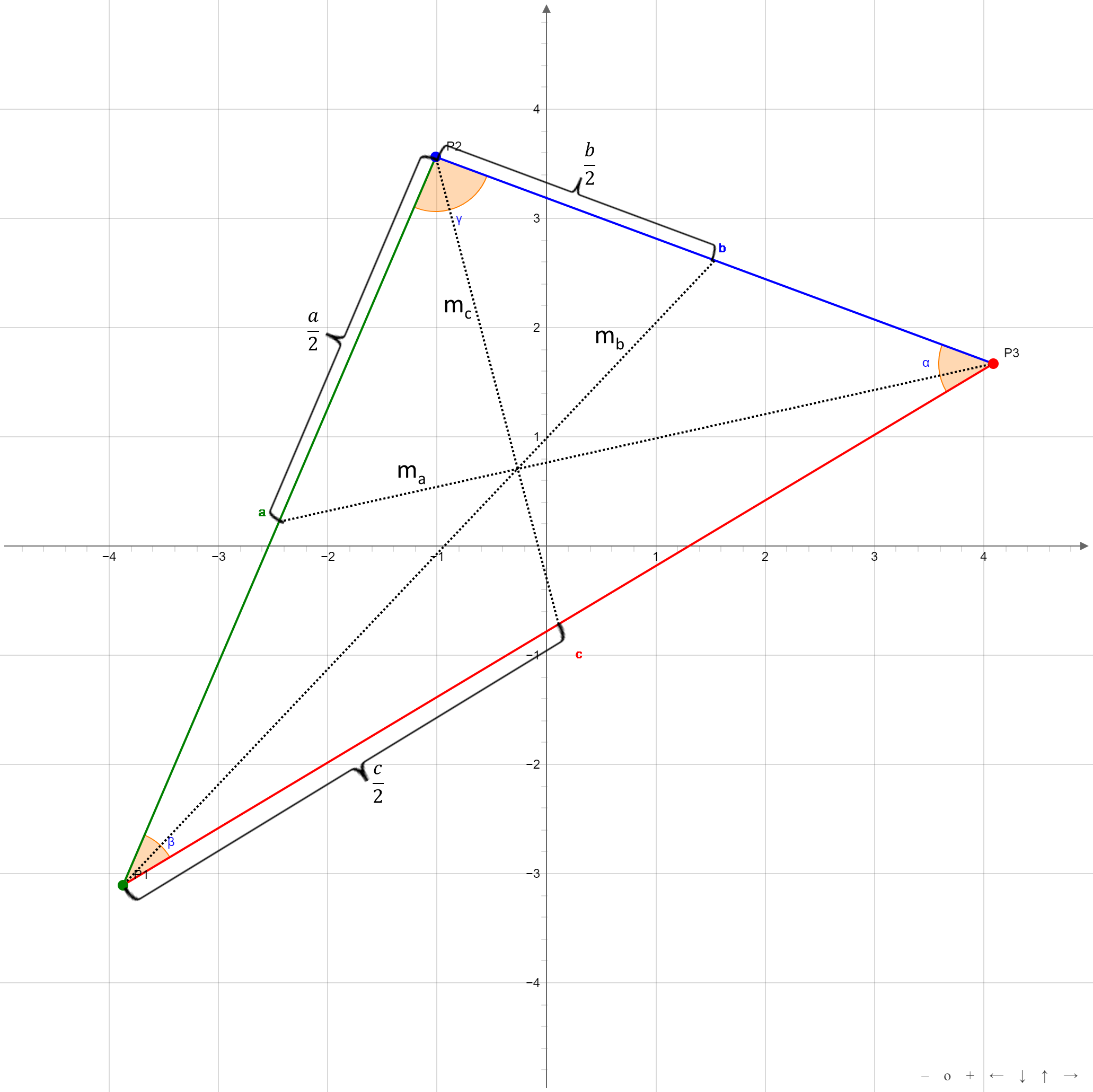
By a median is meant a straight line connecting a vertex of the triangle to the center of the opposite side. The sides of a triangle intersect at the center of gravity of the triangle.

The length of the median of side a is:

$m_{a} = \frac{\sqrt{2 (b^{2} + c^{2}) - a^{2}}}{2}$

The length of the median of side b is:

$m_{b} = \frac{\sqrt{2 (a^{2} + c^{2}) - b^{2}}}{2}$

The length of the median of side c is:

$m_{c} = \frac{\sqrt{2 (a^{2} + b^{2}) - c^{2}}}{2}$

Bisecting

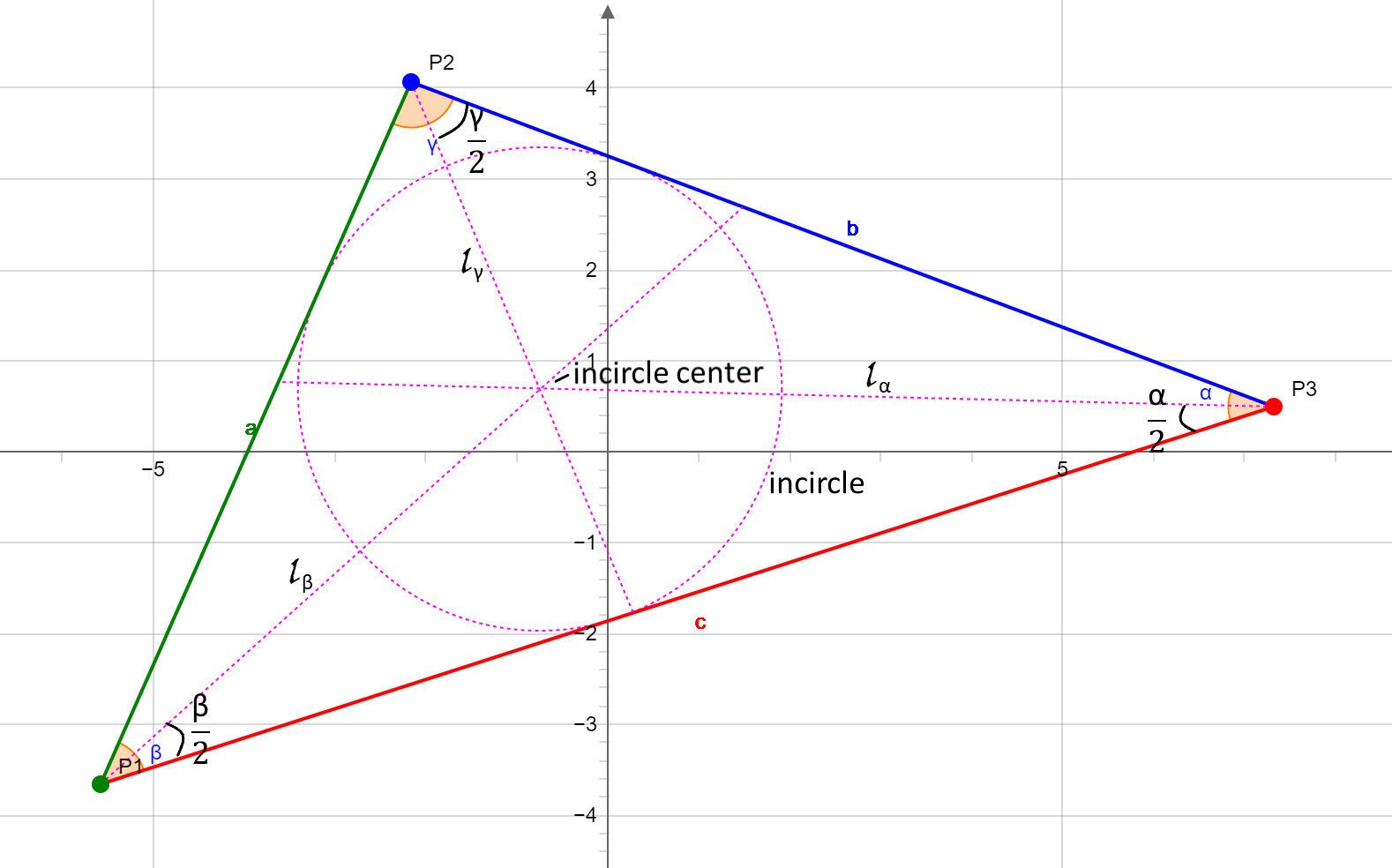
A bisector is a straight line which divides an angle of the triangle into two equal parts. The bisectors of a triangle intersect at the center of the incircle.

The length of the bisector of the angle α is:

$l_{α} = \frac{\sqrt{b c {(b + c)}^{2} - a^{2}}}{b + c}$

The length of the bisector of the angle β is:

$l_{β} = \frac{\sqrt{a c {(a + c)}^{2} - b^{2}}}{a + c}$

The length of the bisector of the angle γ is:

$l_{γ} = \frac{\sqrt{b a {(b + a)}^{2} - c^{2}}}{b + a}$

Height

The height is defined as a straight line at 90° on one side and connecting the side to the opposite corner. The diagram shows the three heights in black dotted lines.

The length of the height on the side a is:

$h_{a} = b \cdot \sin (γ) = c \cdot \sin (β)$

The length of the height on the side b is:

$h_{b} = a \cdot \sin (γ) = c \cdot \sin (α)$

The length of the height on the side c is:

$h_{c} = a \cdot \sin (β) = b \cdot \sin (α)$

Perpendicular bisector

A perpendicular of a side is a line that divides one side of the triangle into two equal parts and is perpendicular to the side. The perpendicular bisector lines of a triangle intersect at the center of the circumcircle.

Circumcircle radius r

The circumcircle is a circle passing through the vertices of the triangle.

$r = \frac{s}{4 \cdot \cos (\frac{α}{2}) \cdot \cos (\frac{β}{2}) \cdot \cos (\frac{γ}{2})}$

with

$s = \frac{1}{2} (a + b + c)$

Incircle radius ρ

The incircle is a circle that touches each side of the triangle.

$ρ = \sqrt{\frac{(s - a) (s - b) (s - c)}{s}}$

Triangle area A

The formula for the triangle area is:

$A = \frac{1}{2} a \cdot b \cdot \sin (γ)$

Triangle circumference U

The formula for the triangle circumference is:

$U = a + b + c$

Heronische area formula

The Heron formula for the triangle area is:

$A = ρ s = \sqrt{s (s - a) (s - b) (s - c)}$

Center line

The center line connects the centers of two triangle sides. It is parallel to the third side and half as long.

Rectangular triangle

The cathetes a and b form a right angle. In oposite to the right angle is the hypotenuse c. The theorem of Pythagoras holds:

$c^{2} = a^{2} + b^{2}$

Area A in the rectangular triangle

The formula for the triangle area in a right angle triangle is:

$A = \frac{a \cdot b}{2}$

Essential for the calculations in general triangle are the cosine and the sine law and the relationship of the trigonometric functions.

Sine law

$\frac{a}{\sin (α)} = \frac{b}{\sin (β)} = \frac{c}{\sin (γ)}$

Cosine law

$a^{2} = b^{2} + c^{2} - 2 b c \cos (α)$

$b^{2} = a^{2} + c^{2} - 2 a c \cos (β)$

$c^{2} = a^{2} + b^{2} - 2 a b \cos (γ)$

Screenshot of the Image

Print or save the image via right mouse click.

Releated sites

Here is a list of of further useful sites:

Index Trigonometric calculations Circle Ellipse Parallelogram Rectangle